题目内容
教材上一例问题如下:
一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表,试建立y与x之间的回归方程.
某同学利用智能手机上的Mathstudio软件研究它时(如图所示),分别采用四种模型,所得结果如下:
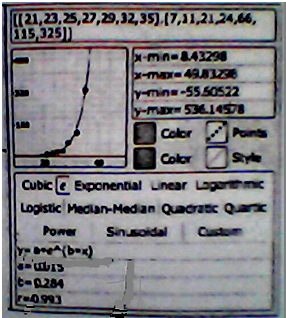
根据上表,易知当选择序号为______的模型是,拟合效果较好.
一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表,试建立y与x之间的回归方程.
| 温度x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
| 产卵数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |

| ① | ② | ③ | ④ | ||||||||||||||||||||||||||
| 模型 | y=ax+b | y=aebx | y=ax2+c | y=ax3+bx2+cx+d | |||||||||||||||||||||||||
| 计算结果 |
|
|
|
|
根据收集的数据,作散点图,如图.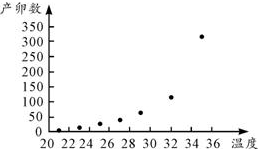
从图中可以看出,样本点并没有分布在某个带状区域内,
因此两个变量不呈线性相关关系,
所以不能直接利用线性回归方程来建立两个变量之间的关系,
根据已有的函数知识,可以发现样本点分布在某一条指数函数曲线y=aebx的附近,其中a,b为待定的参数.
我们可以通过对数变换把指数关系变为线性关系,
令z=lny,则变换后样本点分布在直线z=bx+c(c=lna)的附近,这样可以利用线性回归建立y与x的非线性回归方程了.
变换的样本点分布在一条直线的附近,因此可以用线性回归方程来拟合.
由上表中的数据可得到变换的样本数据表,如下表:
可以求得线性回归直线方程
=0.272x-3.843.
因此红铃虫的产卵数对温度的非线性回归方程=e0.272x-3.843.另一方面,可以认为图中的样本点集中在某二次曲线y=c3x2+c4的附近,其中c3,c4为待定参数,因此可以对温度变量进行变换,即令t=x2,然后建立y与t之间的线性回归方程,从而得到y与x之间的非线性回归方程.
下表是红铃虫的产卵数和对应的温度的平方的线性回归模型拟合表,作出相应的散点图,如图: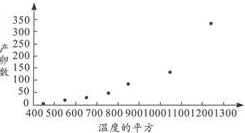
从图中可以看出,y与t的散点图并不分布在一条直线的周围,因此不宜用线性回归方程来拟合它,即不宜用二次函数y=c3x2+c4来拟合x与y之间的关系,因此利用y=aebx来拟合效果较好.
故答案为:②.

从图中可以看出,样本点并没有分布在某个带状区域内,
因此两个变量不呈线性相关关系,
所以不能直接利用线性回归方程来建立两个变量之间的关系,
根据已有的函数知识,可以发现样本点分布在某一条指数函数曲线y=aebx的附近,其中a,b为待定的参数.
我们可以通过对数变换把指数关系变为线性关系,
令z=lny,则变换后样本点分布在直线z=bx+c(c=lna)的附近,这样可以利用线性回归建立y与x的非线性回归方程了.
变换的样本点分布在一条直线的附近,因此可以用线性回归方程来拟合.
由上表中的数据可得到变换的样本数据表,如下表:
| x | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
| z | 1.946 | 2.398 | 3.045 | 3.178 | 4.190 | 4.745 | 5.784 |
| ∧ |
| z |
因此红铃虫的产卵数对温度的非线性回归方程=e0.272x-3.843.另一方面,可以认为图中的样本点集中在某二次曲线y=c3x2+c4的附近,其中c3,c4为待定参数,因此可以对温度变量进行变换,即令t=x2,然后建立y与t之间的线性回归方程,从而得到y与x之间的非线性回归方程.
下表是红铃虫的产卵数和对应的温度的平方的线性回归模型拟合表,作出相应的散点图,如图:

| t | 441 | 529 | 625 | 729 | 841 | 1 024 | 1 225 |
| y | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
故答案为:②.

练习册系列答案
相关题目