题目内容
【题目】某工厂生产甲、乙两种产品，其产量分别为45个与55个，所用原料分别为A、B两种规格的金属板，每张面积分别为2m2与3m2 ． 用A种规格的金属板可造甲种产品3个，乙种产品5个；用B种规格的金属板可造甲、乙两种产品各6个．问A、B两种规格的金属板各取多少张，才能完成计划，并使总的用料面积最省？
【答案】解：设A种原料为x个，B种原料为y个， 由题意有：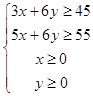 
，
目标函数为Z=2x+3y，
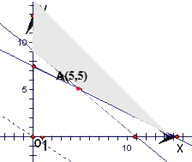
由线性规划知：使目标函数最小的解为（5，5），
即A、B两种原料各取5，5块可保证完成任务，且使总的用料（面积）最小．
【解析】先设A、B两种原料各为x，y个，抽象出约束条件为：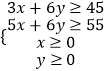 
，建立目标函数，作出可行域，找到最优解求解．
【考点精析】关于本题考查的函数的值域，需要了解求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的才能得出正确答案．
练习册系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
