Question

【题目】如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm. 现有一根玻璃棒l，其长度为40cm.（容器厚度、玻璃棒粗细均忽略不计）

（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；

（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度.

Answer 1

【答案】（1）记玻璃棒与交点为H，则，，没入水中的部分为(cm).

（2），，

记玻璃棒与交点为Q，则

，∴，∴，，

∴，

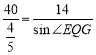没入水中的部分为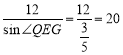(cm)

【解析】

解:（1）由正棱柱的定义，平面，所以平面平面，.

记玻璃棒的另一端落在上点处.

因为，

所以，从而 ，

记与水面的焦点为,过作P1Q1⊥AC, Q1为垂足，

则 P1Q1⊥平面 ABCD，故P1Q1=12，

从而 AP1= .

答：玻璃棒l没入水中部分的长度为16cm.

( 如果将“没入水中部分冶理解为“水面以上部分冶，则结果为24cm)

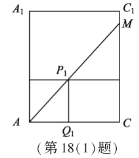
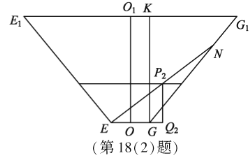
（2）如图，O，O1是正棱台的两底面中心.

由正棱台的定义，OO1⊥平面 EFGH， 所以平面E1EGG1⊥平面EFGH，O1O⊥EG.

同理，平面 E1EGG1⊥平面E1F1G1H1，O1O⊥E1G1.

记玻璃棒的另一端落在GG1上点N处.

过G作GK⊥E1G，K为垂足， 则GK =OO1=32.

因为EG = 14，E1G1= 62，

所以KG1= ，从而.

设则.

因为，所以.

在中，由正弦定理可得，解得.

因为，所以.

于是.

记EN与水面的交点为P2，过 P2作P2Q2⊥EG，Q2为垂足，则 P2Q2⊥平面 EFGH，故P2Q2=12，从而 EP2=.

答:玻璃棒l没入水中部分的长度为20cm.

(如果将“没入水中部分冶理解为“水面以上部分冶，则结果为20cm)