题目内容
【题目】已知函数f（x）=2sin（x+ 
）cosx．
（1）若0≤x≤ 
，求函数f（x）的值域；
（2）设△ABC的三个内角A，B，C所对的边分别为a，b，c，若A为锐角且f（A）= 
，b=2，c=3，求cos（A﹣B）的值．
【答案】
（1）解：f（x）=2sin（x+ 
）cosx
=（sinx+ 
cosx）cosx
=sinxcosx+ cos2x
= 
sin2x+ 
cos2x+
=sin（2x+ ）+ ；
由 
得， 
，
∴ 
，
∴ 
，
即函数f（x）的值域为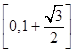 
（2）解：由 
，
得 
，
又由 
，∴ 
，
∴ 
，解得 
；
在△ABC中，由余弦定理a2=b2+c2﹣2bccosA=7，
解得 
；
由正弦定理 
，得 
，
∵b＜a，∴B＜A，∴ 
，
∴cos（A﹣B）=cosAcosB+sinAsinB
= 
【解析】（1）利用三角恒等变换化简f（x），根据x的取值范围即可求出函数f（x）的值域；（2）由f（A）的值求出角A的大小，再利用余弦定理和正弦定理，即可求出cos（A﹣B）的值．
练习册系列答案
相关题目
