[题目]已知动点到定点和的距离之和为.(1)求动点轨迹的方程,(2)设.过点作直线.交椭圆于不同于的两点.直线. 的斜率分别为. .求的值. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知动点到定点和的距离之和为.

(1)求动点轨迹的方程；

(2)设，过点作直线，交椭圆于不同于的两点，直线，的斜率分别为，，求的值.

【答案】（Ⅰ）；（Ⅱ）证明过程详见解析.

【解析】试题分析：本题考查椭圆的基本量间的关系及韦达定理的应用.第一问是考查椭圆的基本量间的关系，比较简单；第二问是直线与椭圆相交于两点，先设出两点坐标，本题的突破口是在消参后的方程中找出两根之和、两根之积，整理斜率的表达式，但是在本问中需考虑直线的斜率是否存在，此题中蕴含了分类讨论的思想的应用.

试题解析：（Ⅰ）由椭圆定义，可知点的轨迹是以为焦点，以为长轴长的椭圆．

由，得．故曲线的方程为． 5分

（Ⅱ）当直线的斜率存在时，设其方程为，

由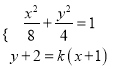，得． 7分

设，，，．

从而． 11分

当直线的斜率不存在时，得，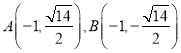

得．

综上，恒有． 12分

练习册系列答案

英语听读空间系列答案

相关题目

【题目】第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行，若集合A={参加北京奥运会比赛的运动员}，集合B={参加北京奥运会比赛的男运动员}．集合C={参加北京奥运会比赛的女运动员}，则下列关系正确的是（　　）
A.AB
B.BC
C.A∩B=C
D.B∪C=A

【题目】已知函数，其中，是自然对数的底数.

（1）当时，求曲线在处的切线方程；

（2）求函数的单调减区间；

（3）若在恒成立，求的取值范围.

【题目】一个几何体的三视图如图所示，则该几何体的表面积为（）
A.38+2π
B.38﹣2π
C.38﹣π
D.38

【题目】设椭圆M： =1（a＞b＞0）的离心率为，点A（a，0），B（0，﹣b），原点O到直线AB的距离为．
（Ⅰ）求椭圆M的方程；
（Ⅱ）设直线l：y=2x+m与椭圆M相交于C、D不同两点，经过线段CD上点E的直线与y轴相交于点P，且有 =0，| |=| |，试求△PCD面积S的最大值．

【题目】椭圆C： =1（a＞b＞0）的左，右焦点分别是F1 ， F2 ，且离心率为，点P为椭圆上一动点，△F1PF2内切圆面积的最大值是．
（1）求椭圆C的方程；
（2）A是椭圆C的左顶点，斜率为k（k＞0）的直线交C于A．M两点，点N在C上，MA⊥NA，且|AM|=|AN|．求△AMN的面积．

【题目】关于x的不等式ax2+（a﹣2）x﹣2≥0（a∈R）
（1）已知不等式的解集为（﹣∞，﹣1]∪[2，+∞），求a的值；
（2）解关于x的不等式ax2+（a﹣2）x﹣2≥0．

【题目】钝角三角形ABC的面积是，AB=1，BC= ，则AC=（）
A.5
B.
C.2
D.1

收入x （万元）	8.2	8.6	10.0	11.3	11.9
支出y （万元）	6.2	7.5	8.0	8.5	9.8

据上表得回归直线方程 = x+ ，其中 =0.76， = ﹣ ，据此估计，该社区一户收入为15万元家庭年支出为（）
A.11.4万元
B.11.8万元
C.12.0万元
D.12.2万元

试题分类