题目内容
【题目】已知函数![]() .
.
(1)讨论函数![]() 在定义域上的单调性;
在定义域上的单调性;
(2)令函数![]() ,是自然对数的底数,若函数
,是自然对数的底数,若函数![]() 有且只有一个零点
有且只有一个零点![]() ,判断
,判断![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 或
或![]() 时,
时,![]() 在
在![]() 上单调递增, 当
上单调递增, 当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减;(2)
上单调递减;(2)![]() .
.
【解析】
(1)求出![]() ,分四种情况讨论
,分四种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)根据函数的单调性求出
的减区间;(2)根据函数的单调性求出![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,由已知函数
,由已知函数![]() 有且仅有一个零点
有且仅有一个零点![]() ,则
,则![]() ,得
,得![]() ,令
,令![]() ,故
,故![]() ,利用导数研究函数的单调性,求出零点的分布情况,从而可求出
,利用导数研究函数的单调性,求出零点的分布情况,从而可求出![]() 的取值范围即可.
的取值范围即可.
(1)由已知![]() ,且
,且![]() ,
,
①当![]() 时,即当
时,即当![]() 时,
时,![]() ,
,
则函数![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() 时,即
时,即![]() 或
或![]() 时,
时,![]() 有两个根,
有两个根,
![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
1°当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
![]() 当
当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
2°当![]() 时,令
时,令![]() ,
,![]() ,
,
解得![]() ,
,
![]() 当
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增;
上单调递增;
3°当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
![]() 当
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减.
上单调递减.
(2)函数![]() ,
,
则![]() ,
,
则![]() ,所以
,所以![]() 在
在![]() 上单调增,
上单调增,
当![]() ,所以
,所以![]()
所以![]() 在
在![]() 上有唯一零点
上有唯一零点![]() ,
,
当![]() ,所以
,所以![]() 为
为![]() 的最小值
的最小值
由已知函数![]() 有且只有一个零点
有且只有一个零点![]() ,则
,则![]()
所以![]() 则
则
则![]() ,得
,得![]() ,
,
令![]() ,所以
,所以![]()
则![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 单调递减,
单调递减,
因为![]() ,
,
所以![]() 在
在![]() 上有一个零点,在
上有一个零点,在![]() 无零点,
无零点,
所以![]() .
.

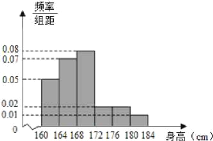
【题目】为了了解学生的学习情况,一次测试中,科任老师从本班中抽取了n个学生的成绩(满分100分,且抽取的学生成绩均在![]() 内)进行统计分析.按照
内)进行统计分析.按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图和频数分布表.
的分组作出频率分布直方图和频数分布表.

频数分布表 | |
| x |
| 4 |
| 10 |
| 12 |
| 8 |
| 4 |
(1)求n,a,x的值;
(2)在选取的样本中,从低于60分的学生中随机抽取两名学生,试问这两名学生在同一组的概率是多少?
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 | b | |
乙班 | c | 30 | |
总计105 |
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
参考公式: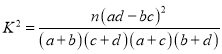
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”