题目内容
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 | b | |
乙班 | c | 30 | |
总计105 |
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
参考公式: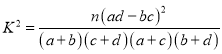
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”
【答案】C
【解析】
根据题意可求出成绩优秀的学生数是![]() ,所以成绩非优秀的学生数是
,所以成绩非优秀的学生数是![]() ,即可求出
,即可求出![]() 的值,判断出
的值,判断出![]() 的真假,再根据列联表求出K2,即可由独立性检验的基本思想判断出
的真假,再根据列联表求出K2,即可由独立性检验的基本思想判断出![]() 的真假.
的真假.
由题意知,成绩优秀的学生数是![]() ,成绩非优秀的学生数是
,成绩非优秀的学生数是![]() ,所以c=20,b=45,选项A,B错误;根据列联表中的数据,得到
,所以c=20,b=45,选项A,B错误;根据列联表中的数据,得到![]() =
=![]() ≈6.109>3.841,因此有95%的把握认为“成绩与班级有关系”,选项C正确.
≈6.109>3.841,因此有95%的把握认为“成绩与班级有关系”,选项C正确.
故选:C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】2018年8月31日,十三届全国人大常委会第五次会议表决通过了关于修改个人所得税法的决定,这是我国个人所得税法自1980年出台以来第七次大修![]() 为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
为了让纳税人尽早享受减税红利,在过渡期对纳税个人按照下表计算个人所得税,值得注意的是起征点变为5000元,即如表中“全月应纳税所得额”是纳税者的月薪金收入减去5000元后的余额.
级数 | 全月应纳税所得额 | 税率 |
1 | 不超过3000元的部分 |
|
2 | 超过3000元至12000元的部分 |
|
3 | 超过12000元至25000元的部分 |
|
|
|
|
某企业员工今年10月份的月工资为15000元,则应缴纳的个人所得税为______元![]()