Question

【题目】

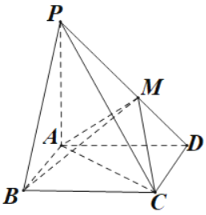
如图4，在四棱锥中，底面是矩形，

平面，，,于点．

(1) 求证：；

(2) 求直线与平面所成的角的余弦值.

Answer 1

【答案】

【解析】

试题(1)要证明线线垂直，可考虑先证明直线和平面垂直，该题先证明平面，从而得到，又，故可证明平面，进而证明；（2）求直线和平面所成的角，需先找后求，同时要有必要的证明过程，该题中直线和平面所成的角不易找到，故可采取转化法，先求点到平面的距离，再利用，求得所求角的正弦值，进而求余弦值．故求点到平面的距离成为解题关键，可利用等体积转化法进行．

试题解析：(1)证明：∵平面，平面,∴.

∵，平面,平面,

∴平面.

∵平面

∴，

∵,,平面,

平面,∴平面.

∵平面,∴.

（2）解：由（1）知，，又，

则是的中点,在Rt△中, 得，

在Rt△中,得,

∴.

设点到平面的距离为，由，

得.解得，

设直线与平面所成的角为，

则，

∴.

∴直线与平面所成的角的余弦值为.