题目内容
【题目】现从某学校高二年级男生中随机抽取![]() 名测量身高,测量发现被测学生身高全部介于
名测量身高,测量发现被测学生身高全部介于![]() 和
和![]() 之间,将测量结果按如下方式分成
之间,将测量结果按如下方式分成![]() 组:第
组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,…,第
,…,第![]() 组
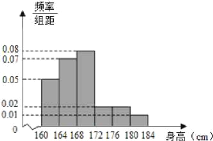
组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.
(1)估计这![]() 名男生身高的中位数和平均数;
名男生身高的中位数和平均数;
(2)求这![]() 名男生当中身高不低于
名男生当中身高不低于![]() 的人数,若在这
的人数,若在这![]() 名身高不低于
名身高不低于![]() 的男生中任意抽取
的男生中任意抽取![]() 人,求这
人,求这![]() 人身高之差不大于
人身高之差不大于![]() 的概率.
的概率.
【答案】(1)中位数为![]() .平均数为168.72(2)
.平均数为168.72(2)![]()
【解析】
(1)设中位数为![]() ,根据频率分布直方图可得
,根据频率分布直方图可得![]() ,解方程可求中位数;平均数
,解方程可求中位数;平均数![]() 每个小矩形的面积
每个小矩形的面积![]() 每个矩形底边中点横坐标之和.
每个矩形底边中点横坐标之和.
(2)根据频率分布直方图可得身高不低于![]() 的有
的有![]() 人,其中,低于
人,其中,低于![]() 的有
的有![]() 人,列举出从这
人,列举出从这![]() 个人中任意抽取
个人中任意抽取![]() 人的所有情况,然后再求出身高差不大于
人的所有情况,然后再求出身高差不大于![]() 的情况,利用古典概型的概率计算公式即可求解.
的情况,利用古典概型的概率计算公式即可求解.
解:(1)设这![]() 名男生身高的中位数为
名男生身高的中位数为![]() ,
,
因为第![]() 组
组![]() 的频率为
的频率为![]() ,第
,第![]() 组
组![]() 的频率为
的频率为![]() ,
,
所以![]() ,且
,且![]() ,
,
解得![]() 所以,这
所以,这![]() 名男生身高的中位数为
名男生身高的中位数为![]() .
.
平均数为![]()
(2)这![]() 名男生当中身高不低于
名男生当中身高不低于![]() 的有
的有![]() 人,
人,
其中,低于![]() 的有
的有![]() 人,记为
人,记为![]() ,另两个人记为
,另两个人记为![]() .
.
从这![]() 个人中任意抽取
个人中任意抽取![]() 人的所有情况列举如下:
人的所有情况列举如下:
![]()
![]()
![]()
![]()
![]() 共有
共有![]() 种情况,
种情况,
这![]() 人身高差不大于
人身高差不大于![]() 即
即![]() 人来自同一组,记为事件
人来自同一组,记为事件![]() ,共包含
,共包含![]() 个基本事件,
个基本事件,
则![]()

 名校课堂系列答案
名校课堂系列答案【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 9 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)该小组发现种子的发芽数![]() (颗)与昼夜温差
(颗)与昼夜温差![]() (℃)呈线性相关关系,试求:线性回归方程
(℃)呈线性相关关系,试求:线性回归方程![]() .
.
(参考公式:线性回归方程![]() 中系数计算公式
中系数计算公式 ,
,![]() .其中
.其中![]() ,
,![]() 表示样本均值.
表示样本均值.
参考数据:![]() ;
;![]() )
)
【题目】《朗读者》是一档文化情感类节目,以个人成长、情感体验、背景故事与传世佳作相结合的方式,选用精美的文字,用最平实的情感读出文字背后的价值,深受人们的喜爱.为了了解人们对该节目的喜爱程度,某调查机构随机调查了![]() ,
,![]() 两个城市各100名观众,得到下面的列联表.
两个城市各100名观众,得到下面的列联表.
非常喜爱 | 喜爱 | 合计 | |
| 60 | 100 | |
| 30 | ||
合计 | 200 |
完成上表,并根据以上数据,判断是否有![]() 的把握认为观众的喜爱程度与所处的城市有关?
的把握认为观众的喜爱程度与所处的城市有关?
附参考公式和数据: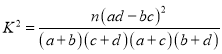 (其中
(其中![]() ).
).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |