题目内容
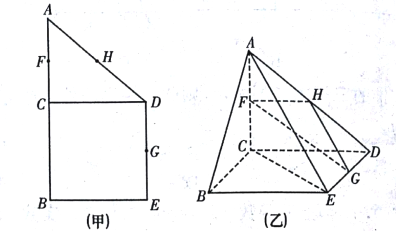
【题目】如图(甲),在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点,现将
的中点,现将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如图(乙).
,如图(乙).
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析(2) ![]()
【解析】试题分析:(1)欲证平面FHG∥平面ABE,只需证明线面平行,故只需要在平面FHG中寻找两条相交直线与平面平行;(2)![]() 这时
这时![]() ,从而
,从而![]() ,
,
过点![]() 作
作![]() 于
于![]() ,连结
,连结![]() .因为
.因为![]() ,所以
,所以![]() 面
面![]() .因为
.因为![]() 面
面![]() ,所以
,所以![]() ,所以
,所以![]() 面
面![]() ,因为
,因为![]() 面
面![]() ,所以
,所以![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角,由
的平面角,由![]() 得
得![]() ,得
,得![]() 所以在
所以在![]() 中
中![]() 即可得解.
即可得解.
试题解析:
(1)证明:由图(甲)结合已知条件知四边形![]() 为正方形,如图(乙),
为正方形,如图(乙),
∵![]() 分别为
分别为![]() 的中点,∴
的中点,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() 面
面![]() ,
, ![]() 面
面![]() .∴
.∴![]() 面
面![]() .
.
同理可得![]() 面
面![]() ,
,
又∵![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)![]() 这时
这时![]() ,
,
从而![]() ,
,
过点![]() 作
作![]() 于
于![]() ,连结
,连结![]() .
.
∵![]() ,∴
,∴![]() 面
面![]() .
.
∵![]() 面
面![]() ,∴
,∴![]() ,∴
,∴![]() 面
面![]() ,
,
∵![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角,
的平面角,
由![]() 得
得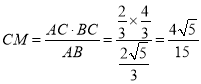 ,
,
∴![]() ,
,
在![]() 中
中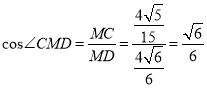 .
.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目