题目内容
【题目】以直角坐标系的原点O为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的参数方程为 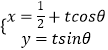 ,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
,(t为参数,0<θ<π),曲线C的极坐标方程为ρsin2α﹣2cosα=0.
(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A,B两点,当θ变化时,求|AB|的最小值.
【答案】
(1)解:∵曲线C的极坐标方程为ρsin2α﹣2cosα=0,
∴ρ2sin2α=2ρcosα,
∴曲线C的直角坐标方程为y2=2x
(2)解:直线l的参数方程 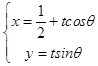 ,(t为参数,0<θ<π),
,(t为参数,0<θ<π),
把直线的参数方程化入y2=2x,得t2sin2θ﹣2tcosθ﹣1=0,
设A,B两点对应的参数分别为t1,t2,
则 ![]() ,t1t2=﹣
,t1t2=﹣ ![]() ,
,
|AB|=|t1﹣t2|= ![]()
= ![]() =
= ![]() ,
,
∴当 ![]() 时,|AB|取最小值2
时,|AB|取最小值2
【解析】(1)曲线C的极坐标方程转化为ρ2sin2α=2ρcosα,由此能求出曲线C的直角坐标方程.(2)把直线的参数方程化入y2=2x,得t2sin2θ﹣2tcosθ﹣1=0,设A,B两点对应的参数分别为t1,t2,则|AB|=|t1﹣t2|= ![]() ,由此能求出当
,由此能求出当 ![]() 时,|AB|取最小值2.
时,|AB|取最小值2.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案【题目】“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
反感 | 10 | ||
不反感 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是 ![]() .
.
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
提示:可参考试卷第一页的公式.
【题目】近来景德镇市棚户区改造进行的如火如荼,加上城市人居环境的不断改善,我市房地产住宅销售价格节节攀升,一部分刚需住户带来了不小的烦恼,下表为我市2017.1﹣2017.5这5月住宅价格与月份的关系.
月份x | 1 | 2 | 3 | 4 | 5 |
住宅价格y | 4.8 | 5.4 | 6.2 | 6.6 | 7 |
(1)通过计算线性相关系数判断住宅价y千元/平米与月份x的线性相关程度(精确到0.01)
(2)用最小二乘法得到的线性回归直线去近似拟合x,y的关系. ①求y关于x的回归方程;②试估计按照这个趋势下去,将在不久的哪个年月份,房价将突破万元/平米的大关.