题目内容
【题目】已知直线![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() 分别与直线
分别与直线![]() ,
,![]() 交于
交于![]() ,其中点
,其中点![]() 在第三象限,点
在第三象限,点![]() 在第二象限,点
在第二象限,点![]() ;
;
(1)若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)直线![]() 交于
交于![]() 点
点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,若
,若![]() 直线的斜率均存在,分别设为
直线的斜率均存在,分别设为![]() ,判断
,判断![]() 是否为定值?若为定值,求出该定值;若不为定值,说明理由.
是否为定值?若为定值,求出该定值;若不为定值,说明理由.
【答案】(1)![]() (2)
(2)![]() 为定值
为定值![]() ,详见解析
,详见解析
【解析】
(1)设直线方程为![]() ,与直线
,与直线![]() ,分别联立,可得
,分别联立,可得![]() 的纵坐标,再由
的纵坐标,再由![]() 的面积为
的面积为![]() ,解方程可得k,进而得到所求直线方程;
,解方程可得k,进而得到所求直线方程;
(2)求得A,B的坐标,设![]() ,运用三点共线的条件:斜率相等,求得
,运用三点共线的条件:斜率相等,求得![]() ,
,![]() ,再由两点的斜率公式,化简整理,计算即可得到所求定值.
,再由两点的斜率公式,化简整理,计算即可得到所求定值.
解:(1)设直线方程为![]() ,
,
与直线![]() ,分别联立,
,分别联立,
可得![]() 的纵坐标分别为
的纵坐标分别为![]() ,
,
∵![]() 的面积为16,
的面积为16,
∴![]()
即![]() ,
,
解得![]() ,
,
∴直线l的方程为![]() ;
;
(2)由(1)可得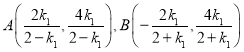 ,
,
又![]() ,设
,设![]() ,
,
由![]() 共线,可得
共线,可得
![]() ,解得
,解得![]() ,
,
即有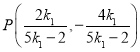 ,
,
由![]() 共线,可得
共线,可得
![]() ,解得
,解得![]() ,
,
即有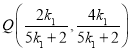 ,
,
则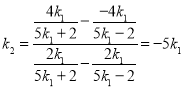 ,
,
即有![]() 为定值
为定值![]() .
.

练习册系列答案
相关题目
【题目】某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B,要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
产品A(件) | 产品B(件) | ||
研制成本与塔载 | 20 | 30 | 计划最大资 |
产品重量(千克/件) | 10 | 5 | 最大搭载 |
预计收益(万元/件) | 80 | 60 |
试问:如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?