题目内容
【题目】设圆
的圆心为
，直线
过点
且与
轴不重合，直线交圆于
，
两点，过点
作
的平行线交
于点
.
（1）证明
为定值，并写出点的轨迹方程；
（2）设点的轨迹为曲线
，直线交于
，
两点，过点且与直线垂直的直线与圆交于
，
两点，求四边形
面积的取值范围.
【答案】（1）证明见解析，
（2）
【解析】
（1）由
，
，故
，所以
，得到
，化简得
，利用椭圆的定义，即可求解；
（2）设
的方程为
，联立方程组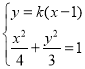
，利用根与系数的关系，结合弦长公式和三角形的面积公式，即可求解．
（1）因为，，故，
所以，故，
又圆
的标准方程为
，
从而
，所以，
由题设得
，
，
，
由椭圆定义可得点
的轨迹方程为.
（2）当与
轴不垂直时，设的方程为，
，
，
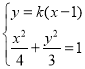由得
，
则
，
，
所以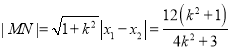
，
过点
且与垂直的直线
，到
的距离为
，
所以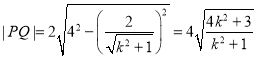
，
故四边形
的面积
，
可得当与轴不垂直时，四边形面积的取值范围为，
当与轴垂直时，其方程为
，
，四边形的面积为
，
综上，四边形面积的取值范围为.
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
