题目内容
【题目】已知椭圆![]() 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过![]() 、
、![]() 、
、![]() 三点.
三点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 交于
交于![]() 、
、![]() 两点,证明直线
两点,证明直线![]() 与直线
与直线![]() 的交点在直线
的交点在直线![]() 上.
上.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
试题(1)当焦点不确定在哪个轴时,可以分别讨论在![]() 轴时,
轴时,![]() ,代入
,代入![]() 点,当在
点,当在![]() 轴时
轴时![]() ,代入
,代入![]() 点解
点解![]() 或
或![]() ,成立的就是椭圆方程;或直接设椭圆的一般式
,成立的就是椭圆方程;或直接设椭圆的一般式![]() ,代入三点的坐标解方程组;
,代入三点的坐标解方程组;
(2)直线方程![]() 与椭圆方程联立,设
与椭圆方程联立,设![]() ,
,![]() ,由根与系数的关系得到
,由根与系数的关系得到![]() 和
和![]() 设直线
设直线![]() 的方程
的方程![]() ,直线
,直线![]() 的方程为
的方程为![]() 后有三种方法,法一,当
后有三种方法,法一,当![]() 时计算交点的纵坐标,并根据直线方程与根与系数的关系证明纵坐标相等,法二是联立直线
时计算交点的纵坐标,并根据直线方程与根与系数的关系证明纵坐标相等,法二是联立直线![]() 与
与![]() 的方程,消去
的方程,消去![]() 后利用根与系数的关系得到交点的横坐标等于4,法三类似于法二,只是先通过根与系数的关系先消去
后利用根与系数的关系得到交点的横坐标等于4,法三类似于法二,只是先通过根与系数的关系先消去![]() ,得到
,得到![]() 与
与![]() 的关系,然后再联立两个方程得到交点横坐标为4.
的关系,然后再联立两个方程得到交点横坐标为4.
试题解析:(1)解法一:当椭圆E的焦点在x轴上时,设其方程为![]() (
(![]() ),
),
则![]() ,又点
,又点![]() 在椭圆
在椭圆![]() 上,得
上,得![]() .解得
.解得![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
当椭圆E的焦点在y轴上时,设其方程为![]() (
(![]() ),
),
则![]() ,又点
,又点![]() 在椭圆
在椭圆![]() 上,得
上,得![]() .
.
解得![]() ,这与
,这与![]() 矛盾.
矛盾.
综上可知,椭圆![]() 的方程为
的方程为![]() .
.
解法二:设椭圆方程为![]() (
(![]() ),
),
将![]() 、
、![]() 、
、![]() 代入椭圆
代入椭圆![]() 的方程,得
的方程,得
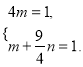 解得
解得![]() ,
,![]() .
.
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)证法一:将直线![]() :
:![]() 代入椭圆
代入椭圆![]() 的方程
的方程![]() 并整理,得
并整理,得![]() ,
,
设直线![]() 与椭圆
与椭圆![]() 的交点
的交点![]() ,
,![]() ,
,
由根与系数的关系,得![]() ,
,![]() .
.
直线![]() 的方程为:
的方程为:![]() ,它与直线
,它与直线![]() 的交点坐标为
的交点坐标为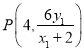 ,
,
同理可求得直线![]() 与直线
与直线![]() 的交点坐标为
的交点坐标为 .
.
下面证明![]() 、
、![]() 两点重合,即证明
两点重合,即证明![]() 、
、![]() 两点的纵坐标相等:
两点的纵坐标相等:
∵![]() ,
,![]() ,
,
∴![]()
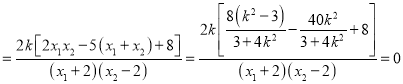 .
.
因此结论成立.
综上可知,直线![]() 与直线
与直线![]() 的交点在直线
的交点在直线![]() 上.
上.
证法二:将直线![]() :
:![]() ,代入椭圆
,代入椭圆![]() 的方程
的方程![]() 并整理,
并整理,
得![]() ,
,
设直线![]() 与椭圆
与椭圆![]() 的交点
的交点![]() ,
,![]() ,
,
由根与系数的关系,得![]() ,
,![]() .
.
直线![]() 的方程为:
的方程为:![]() ,即
,即![]() .
.
直线![]() 的方程为:
的方程为:![]() ,即
,即![]() .
.
由直线![]() 与直线
与直线![]() 的方程消去
的方程消去![]() ,得
,得
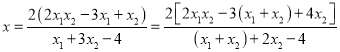
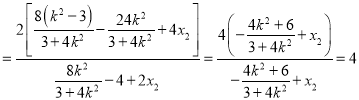 .
.
∴直线![]() 与直线
与直线![]() 的交点在直线
的交点在直线![]() 上.
上.
证法三:将直线![]() :
:![]() ,代入椭圆方程
,代入椭圆方程![]() 并整理,
并整理,
得![]() ,
,
设直线![]() 与椭圆
与椭圆![]() 的交点
的交点![]() ,
,![]() ,
,
由根与系数的关系,得![]() ,
,![]() .
.
消去![]() 得,
得,![]() .
.
直线![]() 的方程为:
的方程为:![]() ,即
,即![]() .
.
直线![]() 的方程为:
的方程为:![]() ,即
,即![]() .
.
由直线![]() 与直线
与直线![]() 的方程消去
的方程消去![]() 得,
得,
 .
.
∴直线![]() 与直线
与直线![]() 的交点在直线
的交点在直线![]() 上.
上.