题目内容
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在棱
在棱![]() 上且
上且![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
在棱![]() 上且
上且![]() ,点
,点![]() 位棱
位棱![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值的大小.
的余弦值的大小.

【答案】(1)见解析.
(2) ![]() .
.
【解析】分析:第一问结合面面垂直的判定定理,寻找图中的垂直的条件,最后归结为线线垂直,在证明线线垂直时,勾股定理也是一个不错的方法,再者就是对二面角的余弦值的求解过程中,利用空间向量来解决,注意对法向量的方向进行分析得出其补角还是其本身是二面角,从而确定是其本身还是其相反数.
详解:(1)在![]() 中,由
中,由![]() ,得
,得![]() ,
,
同理在![]() 中,由
中,由![]() ,得
,得![]() ,
,
所以![]() ,即
,即![]() (亦可通过勾股定理来证明)
(亦可通过勾股定理来证明)
在![]() 中,
中,![]()
在![]() ,
,![]()
所以![]() ,即
,即![]()
(2)由(1)知![]() ,
,![]() ,
,![]() 两两垂直,故以
两两垂直,故以![]() 为坐标原点,以射线
为坐标原点,以射线![]() ,
,![]() ,
,![]() 分别为
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正半轴建立如图所示的空间直角坐标系,得:
轴的正半轴建立如图所示的空间直角坐标系,得:
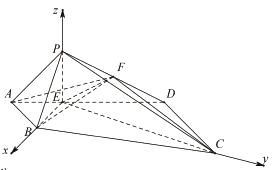
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]()
则: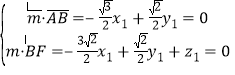
不妨设![]() ,则
,则![]()
设平面![]() 的法向量为
的法向量为![]()
则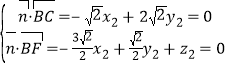 ,
,
不妨设![]() ,则
,则![]()
记二面角![]() 为
为![]() (应为钝角)
(应为钝角)
![]()
故二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目

