题目内容
【题目】“业务技能测试”是量化考核员工绩效等级的一项重要参考依据.某公司为量化考核员工绩效等级设计了A,B两套测试方案,现各抽取![]() 名员工参加A,B两套测试方案的预测试,统计成绩(满分
名员工参加A,B两套测试方案的预测试,统计成绩(满分![]() 分),得到如下频率分布表.
分),得到如下频率分布表.
成绩频率 |
|
|
|
|
|
|
|
方案A |
|
|
|
|
|
|
|
方案B |
|
|
|
|
|
|
|
(1)从预测试成绩在![]() 的员工中随机抽取
的员工中随机抽取![]() 人,记参加方案A的人数为
人,记参加方案A的人数为![]() ,求
,求![]() 的最有可能的取值;
的最有可能的取值;
(2)由于方案A的预测试成绩更接近正态分布,该公司选择方案A进行业务技能测试.测试后,公司统计了若干部门测试的平均成绩![]() 与绩效等级优秀率
与绩效等级优秀率![]() ,如下表所示:
,如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据数据绘制散点图,初步判断,选用![]() 作为回归方程.令
作为回归方程.令![]() ,经计算得
,经计算得![]() ,
,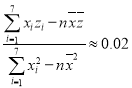 ,
,![]() .
.
(ⅰ)若某部门测试的平均成绩为![]() ,则其绩效等级优秀率的预报值为多少?
,则其绩效等级优秀率的预报值为多少?
(ⅱ)根据统计分析,大致认为各部门测试平均成绩![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,求某个部门绩效等级优秀率不低于
,求某个部门绩效等级优秀率不低于![]() 的概率为多少?
的概率为多少?
参考公式与数据:(1)![]() ,
,![]() ,
,![]() .
.
(2)线性回归方程![]() 中,
中,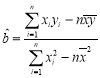 ,
,![]() .
.
(3)若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【答案】(1)![]() 最有可能的取值为1.(2)(ⅰ)0.498.(ⅱ)0.1587.
最有可能的取值为1.(2)(ⅰ)0.498.(ⅱ)0.1587.
【解析】
(1)随机变量![]() 服从超几何分布,记这6人中接受方案
服从超几何分布,记这6人中接受方案![]() 预测试的人数为
预测试的人数为![]() ,则
,则![]() ,其中
,其中![]() ,可得
,可得![]() ,即可得答案;
,即可得答案;
(2)(i)依题意,![]() 两边取对数,得
两边取对数,得![]() ,求得回归方程故
,求得回归方程故![]() ,再将当
,再将当![]() 代入,即可得答案;
代入,即可得答案;
(ii)由(i)及提供的参考数据可知,![]() ,记“绩效等级优秀率不低于0.78”为事件
,记“绩效等级优秀率不低于0.78”为事件![]() ,则
,则![]() ,即可得答案;
,即可得答案;
(1)预测试成绩在![]() 的员工中,
的员工中,
接受方案![]() 测试的有
测试的有![]() 人;
人;
接受方案![]() 测试的有
测试的有![]() 人.
人.
依题意,随机变量![]() 服从超几何分布,记这6人中接受方案
服从超几何分布,记这6人中接受方案![]() 预测试的人数为
预测试的人数为![]() ,
,
则![]() ,其中
,其中![]() .
.
![]() ,
,
得![]() ,即
,即![]() 的可能性最大,故
的可能性最大,故![]() 最有可能的取值为1.
最有可能的取值为1.
(2)(i)依题意,![]() 两边取对数,得
两边取对数,得![]() ,
,
即![]() ,其中
,其中![]() ,
,
由提供的参考数据,可知![]() ,又
,又![]() ,故
,故![]() ,
,
由提供的参考数据,可得![]() ,
,
故![]() ,当
,当![]() 时,
时,![]() .
.
(ii)由(i)及提供的参考数据可知,![]() .
.
![]() ,即
,即![]() ,可得
,可得![]() ,即
,即![]() .
.
又![]() ,且
,且![]() ,
,
由正态分布的性质,得![]() ,
,
记“绩效等级优秀率不低于0.78”为事件![]() ,则
,则![]() ,
,
所以绩效等级优秀率不低于0.78的概率等于0.1587.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】某农科院为试验冬季昼夜温差对反季节大豆新品种发芽的影响,对温差与发芽率之间的关系进行统计分析研究,记录了6天昼夜温差与实验室中种子发芽数的数据如下:
日期 | 1月1日 | 1月2日 | 1月3日 | 1月4日 | 1月5日 | 1月6日 |
温差 | 10 | 11 | 12 | 13 | 8 | 9 |
发芽数 | 26 | 27 | 30 | 32 | 21 | 24 |
他们确定的方案是先从这6组数据中选出2组,用剩下的4组数据求回归方程,再用选取的两组数据进行检验.
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若由线性回归方程得到的估计数据与实际数据的误差不超过1粒,则认为得到的线性回归方程是可靠的.请根据1月2,3,4,5日的数据求出![]() 关于
关于![]() 的线性回归方程(保留两位小数),并检验此方程是否可靠.
的线性回归方程(保留两位小数),并检验此方程是否可靠.
参考公式: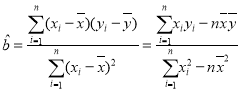 ,
,![]()
【题目】某公司为提高市场销售业绩,促进某产品的销售,随机调查了该产品的月销售单价![]() (单位:元/件)及相应月销量
(单位:元/件)及相应月销量![]() (单位:万件),对近5个月的月销售单价
(单位:万件),对近5个月的月销售单价![]() 和月销售量
和月销售量![]() 的数据进行了统计,得到如下表数据:
的数据进行了统计,得到如下表数据:
月销售单价 | 9 |
| 10 |
| 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)建立![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(Ⅱ)该公司开展促销活动,当该产品月销售单价为7元/件时,其月销售量达到18万件,若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过![]() 万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
万件,则认为所得到的回归直线方程是理想的,试问:(Ⅰ)中得到的回归直线方程是否理想?
(Ⅲ)根据(Ⅰ)的结果,若该产品成本是5元/件,月销售单价![]() 为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
为何值时(销售单价不超过11元/件),公司月利润的预计值最大?
参考公式:回归直线方程![]() ,其中
,其中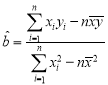 ,
,![]() .
.
参考数据:![]() ,
,