题目内容
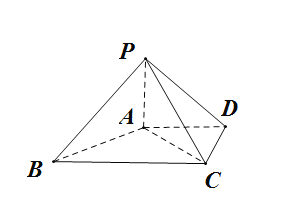
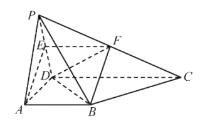
【题目】在四棱锥P﹣ABCD中,△PAB是边长为2的等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,BC=CD=1,PD![]() .
.

(1)证明:AB⊥PD.
(2)求二面角A﹣PB﹣C的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)根据勾股定理的逆定理、线面垂直的判定定理、线面垂直的性质进行证明即可;
(2)由AD2+BD2=AB2,可得AD⊥BD,以D为原点,DA为x轴,DB为y轴,DP为z轴,建立空间直角坐标系,根据空间向量夹角公式进行求解即可.
(1)证明:连结BD,
∵在四棱锥P﹣ABCD中,△PAB是边长为2的等边三角形,
底面ABCD为直角梯形,AB∥CD,AB⊥BC,BC=CD=1,PD![]() .
.
∴BD=AD![]() ,
,
∴AD2+PD2=AP2,BD2+PD2=PB2,
∴AD⊥PD,BD⊥PD,
∵AD∩BD=D,∴PD⊥平面ABCD,
∵AB平面ABCD,∴AB⊥PD.
(2)解:∵AD2+BD2=AB2,∴AD⊥BD,
以D为原点,DA为x轴,DB为y轴,DP为z轴,建立空间直角坐标系,
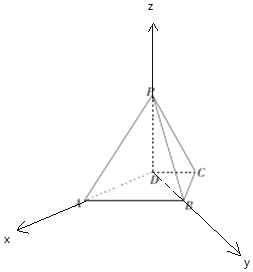
则A(![]() ,0,0),B(0,
,0,0),B(0,![]() ,0),C(
,0),C(![]() ,0),P(0,0,
,0),P(0,0,![]() ),
),
![]() (
(![]() ),
),![]() (0,
(0,![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ,
,![]() ),
),
设平面ABP的法向量![]() (x,y,z),
(x,y,z),
则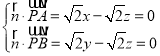 ,取x=1,得
,取x=1,得![]() (1,1,1),
(1,1,1),
设平面PBC的法向量![]() ,
,
则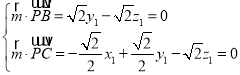 ,取
,取![]() ,得
,得![]() (﹣1,1,1),
(﹣1,1,1),
设二面角A﹣PB﹣C的平面角为θ,
则二面角A﹣PB﹣C的余弦值为:cosθ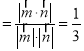 .
.

 阅读快车系列答案
阅读快车系列答案【题目】某人经营淡水池塘养草鱼,根据过去![]() 期的养殖档案,该池塘的养殖重量
期的养殖档案,该池塘的养殖重量![]() (百斤)都在
(百斤)都在![]() 百斤以上,其中不足
百斤以上,其中不足![]() 百斤的有
百斤的有![]() 期,不低于
期,不低于![]() 百斤且不超过
百斤且不超过![]() 百斤的有
百斤的有![]() 期,超过
期,超过![]() 百斤的有
百斤的有![]() 期.根据统计,该池塘的草鱼重量的增加量
期.根据统计,该池塘的草鱼重量的增加量![]() (百斤)与使用某种饵料的质量
(百斤)与使用某种饵料的质量![]() (百斤)之间的关系如图所示.
(百斤)之间的关系如图所示.
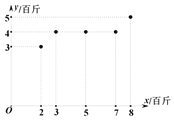
(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 关于
关于![]() 的回归方程
的回归方程![]() ;如果此人设想使用某种饵料
;如果此人设想使用某种饵料![]() 百斤时,草鱼重量的增加量须多于
百斤时,草鱼重量的增加量须多于![]() 百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.
百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.
(2)养鱼的池塘对水质含氧量与新鲜度要求较高,某商家为该养殖户提供收费服务,即提供不超过![]() 台增氧冲水机,每期养殖使用的冲水机运行台数与鱼塘的鱼重量
台增氧冲水机,每期养殖使用的冲水机运行台数与鱼塘的鱼重量![]() 有如下关系:
有如下关系:
鱼的重量(单位:百斤) |
|
|
|
冲水机只需运行台数 |
|
|
|
若某台增氧冲水机运行,则商家每期可获利![]() 千元;若某台冲水机未运行,则商家每期亏损
千元;若某台冲水机未运行,则商家每期亏损![]() 千元.视频率为概率,商家欲使每期冲水机总利润的均值达到最大,应提供几台增氧冲水机?
千元.视频率为概率,商家欲使每期冲水机总利润的均值达到最大,应提供几台增氧冲水机?
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为
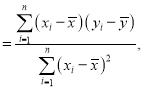
![]()
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中 ,
,![]() .
.
【题目】“业务技能测试”是量化考核员工绩效等级的一项重要参考依据.某公司为量化考核员工绩效等级设计了A,B两套测试方案,现各抽取![]() 名员工参加A,B两套测试方案的预测试,统计成绩(满分
名员工参加A,B两套测试方案的预测试,统计成绩(满分![]() 分),得到如下频率分布表.
分),得到如下频率分布表.
成绩频率 |
|
|
|
|
|
|
|
方案A |
|
|
|
|
|
|
|
方案B |
|
|
|
|
|
|
|
(1)从预测试成绩在![]() 的员工中随机抽取
的员工中随机抽取![]() 人,记参加方案A的人数为
人,记参加方案A的人数为![]() ,求
,求![]() 的最有可能的取值;
的最有可能的取值;
(2)由于方案A的预测试成绩更接近正态分布,该公司选择方案A进行业务技能测试.测试后,公司统计了若干部门测试的平均成绩![]() 与绩效等级优秀率
与绩效等级优秀率![]() ,如下表所示:
,如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据数据绘制散点图,初步判断,选用![]() 作为回归方程.令
作为回归方程.令![]() ,经计算得
,经计算得![]() ,
,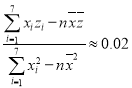 ,
,![]() .
.
(ⅰ)若某部门测试的平均成绩为![]() ,则其绩效等级优秀率的预报值为多少?
,则其绩效等级优秀率的预报值为多少?
(ⅱ)根据统计分析,大致认为各部门测试平均成绩![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,求某个部门绩效等级优秀率不低于
,求某个部门绩效等级优秀率不低于![]() 的概率为多少?
的概率为多少?
参考公式与数据:(1)![]() ,
,![]() ,
,![]() .
.
(2)线性回归方程![]() 中,
中,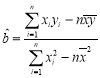 ,
,![]() .
.
(3)若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() .
.