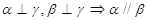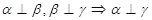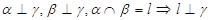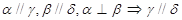题目内容
(本小题满分10分)
在三棱锥S—ABC中,底面是边长为2的正三角形,点S在
底面ABC上的射影O恰是BC的中点,侧棱SA和底面成45°角.
(1) 若D为侧棱SA上一点,当为何值时,BD⊥AC;
(2) 求二面角S—AC—B的余弦值大小.
在三棱锥S—ABC中,底面是边长为2的正三角形,点S在
底面ABC上的射影O恰是BC的中点,侧棱SA和底面成45°角.
(1) 若D为侧棱SA上一点,当为何值时,BD⊥AC;
(2) 求二面角S—AC—B的余弦值大小.

(1)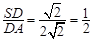 . (2)
. (2)  .
.
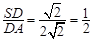 . (2)
. (2)  .
.本试题主要是考查了立体几何中线线垂直的证明以及二面角的平面角的求解的综合运用。
(1)建立合理的空间直角坐标系,然后表示向量的坐标,利用向量的数量积为零来证明垂直。
(2)结合平面的法向量的坐标,和法向量的夹角公式,来表示二面角的平面角的大小。
以O点为原点,OC为x轴,OA为y轴,OS为z轴建立空间直角坐标系.因为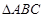 是边长为
是边长为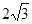 的正三角形,又
的正三角形,又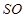 与底面所成角为
与底面所成角为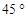 ,所以∠
,所以∠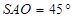 ,所以
,所以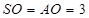 .
.
所以O(0,0,0),C(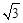 ,0,0),A(0,3,0),S(0,0,3),B(-
,0,0),A(0,3,0),S(0,0,3),B(-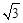 ,0,0).…………………………2分
,0,0).…………………………2分

(1)设AD=a,则D(0,3- a,
a, a),所以
a),所以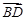 =(-
=(-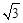 ,3-
,3- a,
a, a),
a),
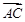 =(
=(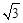 ,-3,0).若BD⊥AC,则
,-3,0).若BD⊥AC,则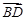 ·
·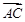 =3-3(3-
=3-3(3- a)=0,
a)=0,
解得a=2 ,而AS=3
,而AS=3 ,所以SD=
,所以SD= ,
,
所以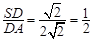 .………………………5分
.………………………5分
(2)因为 =(0,-3,3),
=(0,-3,3),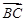 =(2
=(2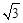 ,0,0)
,0,0)
设平面ACS的法向量为n1=(x,y,z),
则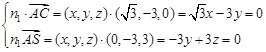
令z=1,则x=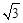 ,y=1,所以n1=(
,y=1,所以n1=(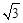 ,1,1)………………………………………………………7分
,1,1)………………………………………………………7分
而平面ABC的法向量为n2=(0,0,1), ………………………………………………………………8分
所以cos<n1,n2>= ,又显然所求二面角的平面角为锐角,
,又显然所求二面角的平面角为锐角,
故所求二面角的余弦值的大小为 .……………………………………………………………10分
.……………………………………………………………10分
(1)建立合理的空间直角坐标系,然后表示向量的坐标,利用向量的数量积为零来证明垂直。
(2)结合平面的法向量的坐标,和法向量的夹角公式,来表示二面角的平面角的大小。
以O点为原点,OC为x轴,OA为y轴,OS为z轴建立空间直角坐标系.因为
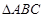 是边长为
是边长为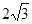 的正三角形,又
的正三角形,又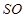 与底面所成角为
与底面所成角为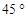 ,所以∠
,所以∠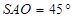 ,所以
,所以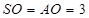 .
.所以O(0,0,0),C(
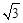 ,0,0),A(0,3,0),S(0,0,3),B(-
,0,0),A(0,3,0),S(0,0,3),B(-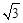 ,0,0).…………………………2分
,0,0).…………………………2分
(1)设AD=a,则D(0,3-
 a,
a, a),所以
a),所以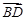 =(-
=(-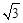 ,3-
,3- a,
a, a),
a),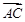 =(
=(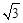 ,-3,0).若BD⊥AC,则
,-3,0).若BD⊥AC,则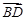 ·
·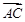 =3-3(3-
=3-3(3- a)=0,
a)=0,解得a=2
 ,而AS=3
,而AS=3 ,所以SD=
,所以SD= ,
,所以
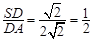 .………………………5分
.………………………5分(2)因为
 =(0,-3,3),
=(0,-3,3),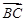 =(2
=(2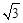 ,0,0)
,0,0)设平面ACS的法向量为n1=(x,y,z),
则
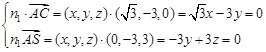
令z=1,则x=
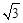 ,y=1,所以n1=(
,y=1,所以n1=(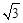 ,1,1)………………………………………………………7分
,1,1)………………………………………………………7分而平面ABC的法向量为n2=(0,0,1), ………………………………………………………………8分
所以cos<n1,n2>=
 ,又显然所求二面角的平面角为锐角,
,又显然所求二面角的平面角为锐角,故所求二面角的余弦值的大小为
 .……………………………………………………………10分
.……………………………………………………………10分
练习册系列答案
相关题目
 中,已知
中,已知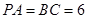 ,
,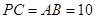 ,
, ,
,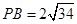 ,
, 是线段
是线段 上一点,
上一点,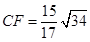 ,点
,点 在线段
在线段 上,且
上,且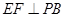 。
。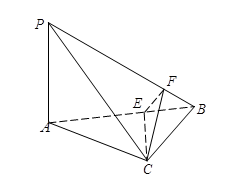
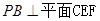 ;
;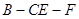 的平面角的正弦值。
的平面角的正弦值。
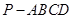 的底面是正方形,
的底面是正方形,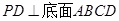 ,点E在棱PB上。
,点E在棱PB上。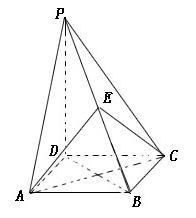
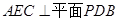 ;
;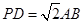 且E为PB的中点时,求AE与平
且E为PB的中点时,求AE与平 ,∠ACB=900,M是AA1的中点,N是BC1的中点.
,∠ACB=900,M是AA1的中点,N是BC1的中点.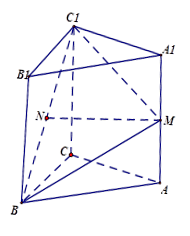
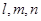 为三条不同的直线,
为三条不同的直线,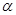 为一个平面,下列命题中正确的个数是 ( )
为一个平面,下列命题中正确的个数是 ( )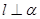 ,则
,则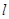 与
与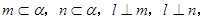 则
则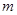 ,
,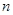 ,
,
 ,
,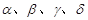 表示平面,
表示平面,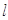 为直线,下列命题中为真命题的是 ( )
为直线,下列命题中为真命题的是 ( )