题目内容
【题目】如图,在四棱锥![]() 中,棱
中,棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.

【答案】(1) 见解析(2) ![]()
【解析】试题分析:(1)取![]() 中点
中点![]() ,连接
,连接![]() ,利用线面垂直的性质,得到
,利用线面垂直的性质,得到![]() ,进而得到
,进而得到![]() 平面
平面![]() ,又根据三角形的性质,证得
,又根据三角形的性质,证得![]() ,即可证明
,即可证明![]() 平面
平面![]() ;
;
(2)解:由(1)知, ![]() 是三棱锥
是三棱锥![]() 的高,再利用三棱锥的体积公式,即可求解几何体的体积.
的高,再利用三棱锥的体积公式,即可求解几何体的体积.
试题解析:
(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,∵
,∵![]() 底面
底面![]() ,
, ![]() 底面
底面![]() ,
, ![]()
![]() ,且
,且![]()
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() .
.
又∵![]() ,H为PB的中点,
,H为PB的中点, ![]() ,又
,又![]() ,
, ![]() 平面
平面![]() ,在
,在![]() 中,
中, ![]() 分别为
分别为![]() 中点,
中点, ![]() ,又
,又![]() ,
, ![]() ,
,
![]() ,
, ![]() ∴四边形
∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() 、
、![]() 平面
平面![]() .
.
(2)解:由(1)知, ![]() ,∴
,∴![]() ,又
,又![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,
, ![]() 是三棱锥
是三棱锥![]() 的高,又可知四边形
的高,又可知四边形![]() 为矩形,且
为矩形,且![]() ,
, ![]() ,所以
,所以![]()
![]() .
.
另解: ![]() 是
是![]() 的中点,∴
的中点,∴![]() 到平面
到平面![]() 的距离是
的距离是![]() 到平面
到平面![]() 的距离的一半,
的距离的一半,
所以![]() .
.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案【题目】某中学每年暑假举行“学科思维讲座”活动,每场讲座结束时,所有听讲这都要填写一份问卷调查.2017年暑假某一天五场讲座收到的问卷份数情况如下表:
学科 | 语文 | 数学 | 英语 | 理综 | 文综 |
问卷份数 |
|
|
|
|
|
用分层抽样的方法从这一天的所有问卷中抽取![]() 份进行统计,结果如下表:
份进行统计,结果如下表:
满意 | 一般 | 不满意 | |
语文 |
|
|
|
数学 |
| 1 |
|
英语 |
|
|
|
理综 |
|
|
|
文综 |
|
|
|
(1)估计这次讲座活动的总体满意率;
(2)求听数学讲座的甲某的调查问卷被选中的概率;
(3)若想从调查问卷被选中且填写不满意的人中再随机选出![]() 人进行家访,求这
人进行家访,求这![]() 人中选择的是理综讲座的人数的分布列.
人中选择的是理综讲座的人数的分布列.
【题目】现在的人基本每天都离不开手机,许多人手机一旦不在身边就不舒服,几乎达到手机二十四小时不离身,这类人群被称为“手机控”,这一群体在大学生中比较突出.为了调查大学生每天使用手机的时间,某调查公司针对某高校男生、女生各25名学生进行了调查,其中每天使用手机时间超过8小时的被称为:“手机控”,否则被称为“非手机控”.调查结果如下:
手机控 | 非手机控 | 合计 | |
女生 | 5 | ||
男生 | 10 | ||
合计 | 50 |
(1)将上面的列联表补充完整,再判断是否有99.5%的把握认为“手机控”与性别有关,说明你的理由;
(2)现从被调查的男生中按分层抽样的方法选出5人,再从这5人中随机选取3人参加座谈会,记这3人中“手机控”的人数为![]() ,试求
,试求![]() 的分布列与数学期望.
的分布列与数学期望.
参考公式: 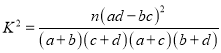 ,其中
,其中![]() .
.