题目内容
5.下列命题中,假命题为( )| A. | 存在四边相等的四边形不是正方形 | |
| B. | 设x,y∈R,则“(x-y)•x2<0”是“x<y”的必要而不充分条件 | |
| C. | 若x,y∈R,且x+y>2,则x,y至少有一个大于1 | |
| D. | 命题:?n∈N,2n>1000的否定是:?n∈N,2n≤1000 |
分析 举出正例,可判断A;分析两个命题的充要性,可判断B;利用反证法,可判断C的真假;写出原命题的否定,可判断D的真假.
解答 解:如果一个菱形的内角不为直角,则满足四边相等,且不为正方形,故A为真命题;
设x,y∈R,则“(x-y)•x2<0”?“x<y,且x≠0”是“x<y”的充分不必要条件,故B为假命题;
若x,y都小于等于1,则x+y≤2,故若x,y∈R,且x+y>2,则x,y至少有一个大于1,故C为真命题;
命题:?n∈N,2n>1000的否定是:?n∈N,2n≤1000,故D为真命题;
故选:B
点评 本题考查的知识点是命题的真假判断与应用,全称(特称)命题,反证法,难度不大,属于基础题.

练习册系列答案
相关题目
15.在△ABC中,若c2+ab=a2+b2,则角C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
13.散点图在回归分析过程中的作用是( )
| A. | 查找个体个数 | B. | 粗略判断变量是否线性相关 | ||
| C. | 探究个体分类 | D. | 比较个体数据大小关系 |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),两个焦点分别为F1、F2,若在第一象限内双曲线上存在一点P,使得在△PF1F2中,∠PF1F2=30°,∠PF2F1=90°,则此双曲线的渐近线方程为( )
| A. | $y=±\frac{{\sqrt{2}}}{2}x$ | B. | $y=±\sqrt{2}x$ | C. | $y=±\sqrt{3}x$ | D. | y=±2x |
14.设6件产品中有4件合格品2件不合格品,从中任意取2件,则其中至少一件是不合格品的概率为( )
| A. | 0.4 | B. | 0.5 | C. | 0.6 | D. | 0.7 |
15.已知c>b>a,c+b+a=0,则下列不等式一定成立的是( )
| A. | c2>b2>a2 | B. | c|b|>a|b| | C. | bc>ac | D. | ac>ab |
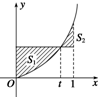 在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).
在区间[0,1]上给定曲线y=x2,如图所示,0<t<1,S1,S2是t的函数,则函数g(t)=S1+S2的单调递增区间为($\frac{1}{2}$,1).