题目内容
甲乙两人各有一个箱子,甲的箱子里面放有 个红球,
个红球, 个白球(
个白球( ,且
,且 );乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
);乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?并求甲获胜的概率的最大值.
(2) 当甲获胜的概率取得最大值时,求取出的3个球中红球个数 的分布列.
的分布列.
 个红球,
个红球, 个白球(
个白球( ,且
,且 );乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
);乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.(1)试问甲如何安排箱子里两种颜色球的个数,才能使自己获胜的概率最大?并求甲获胜的概率的最大值.
(2) 当甲获胜的概率取得最大值时,求取出的3个球中红球个数
 的分布列.
的分布列.(1) 甲应在箱子里放2个红球2个白球才能使自己获胜的概率最大. 他获胜的概率的最大值为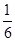 (2)
(2)
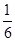 (2)
(2)| ξ | 0 | 1 | 2 | 3 |
| P | 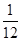 | 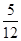 | 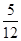 | 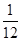 |
试题分析:(1)要想使取出的3个球颜色都不相同,则乙必须取出黄球,甲取出的两个球为一个红球一个白球,乙取出黄球的概率是
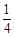 ,甲取出的两个球为一个红球一个白球的概率是
,甲取出的两个球为一个红球一个白球的概率是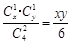 ,所以取出的3个球颜色全不相同的概率是
,所以取出的3个球颜色全不相同的概率是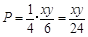 ,即甲获胜的概率为
,即甲获胜的概率为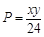 ,由
,由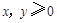 ,且
,且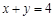 ,所以
,所以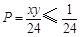
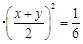 ,当
,当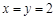 时取等号,即甲应在箱子里放2个红球2个白球才能使自己获胜的概率最大. 他获胜的概率的最大值为
时取等号,即甲应在箱子里放2个红球2个白球才能使自己获胜的概率最大. 他获胜的概率的最大值为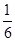 . 7分
. 7分(2)ξ的取值为0,1,2,3.
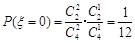 ,
, 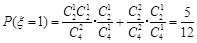 ,
,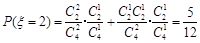 ,
, 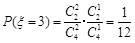 ,
,ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | 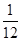 | 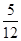 | 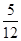 | 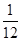 |
点评:第一问求概率最值问题结合了不等式,学生不易想到,第二问求分布列的题目主要分3步:1,找到随机变量可以取得值,2,求出各随机变量对应的概率,3,将上述数据汇总成分布列

练习册系列答案
相关题目
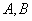 为两个事件,且
为两个事件,且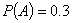 ,
,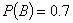 ,则( )
,则( )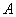 与
与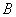 互斥
互斥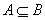
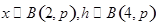 ,若
,若 ,则
,则 的值为( )
的值为( )




 表示抽到“极幸福”的人数, 求
表示抽到“极幸福”的人数, 求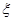 的分布列,并求李明在一年内领到驾照的概率.
的分布列,并求李明在一年内领到驾照的概率.
 为区间
为区间 上的
上的 等分点,直线
等分点,直线 ,
, ,
, 和曲线
和曲线 所围成的区域为
所围成的区域为 ,图中
,图中 ,在
,在