题目内容
(本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在8,9,10环,且每次射击击中与否互不影响.甲、乙射击命中环数的概率如表:
(Ⅰ)若甲、乙两运动员各射击1次,求甲运动员击中8环且乙运动员击中9环的概率;
(Ⅱ)若甲、乙两运动员各自射击2次,求这4次射击中恰有3次击中9环以上(含9环)的概率.
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在8,9,10环,且每次射击击中与否互不影响.甲、乙射击命中环数的概率如表:
| | 8环 | 9环 | 10环 |
| 甲 | 0.2 | 0.45 | 0.35 |
| 乙 | 0.25 | 0.4 | 0.35 |
(Ⅱ)若甲、乙两运动员各自射击2次,求这4次射击中恰有3次击中9环以上(含9环)的概率.
(1) 0.08.
(2) 甲、乙两运动员各自射击两次,这4次射击中恰有3次击中9环以上的概率为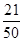
(2) 甲、乙两运动员各自射击两次,这4次射击中恰有3次击中9环以上的概率为
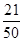
试题分析:解:(Ⅰ)由已知甲射击击中8环的概率为0.2,乙射击击中9环的概率为0.4,则所求事件的概率为 P=0.2×0.4=0.08. 3分
(Ⅱ)记“甲运动员射击一次,击中9环以上(含9环)”为事件A,“乙运动员射击1次,击中9环以上(含9环)”为事件B,则
P(A)=0.35+0.45=0.8,P(B)=0.35+0.4=0.75. 5分
“甲、乙两运动员各自射击两次,这4次射击中恰有3次击中9环以上(含9环)”包含甲击中2次、乙击中1次,与甲击中1次、乙击中2次两个事件,这两个事件为互斥事件.
甲击中2次、乙击中1次的概率为
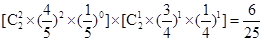 ; 8分
; 8分甲击中1次、乙击中2次的概率为
 . 11分
. 11分故所求概率为
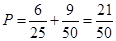 . 12分
. 12分答:甲、乙两运动员各自射击两次,这4次射击中恰有3次击中9环以上的概率为
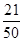 .
.点评:解决的关键是对于概率的加法公式和乘法公式的准确运用,属于基础题。

练习册系列答案
相关题目
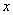 ,
,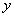 .现 从中任取3张卡片,假设每张卡片被取出的可能性相同.
.现 从中任取3张卡片,假设每张卡片被取出的可能性相同.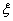 表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时
表示三张卡片上的数字之和.当三张卡片中含有字母时,则约定:有一个字母和二个相同数字时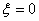 ,求
,求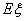 .
. 个红球,
个红球, 个白球(
个白球( ,且
,且 );乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜.
);乙的箱子里面放有2个红球,1个白球,1个黄球.现在甲从自己的箱子里任取2个球,乙从自己的箱子里任取1个球.若取出的3个球颜色都不相同,则甲获胜. 的分布列.
的分布列. 服从二项分布
服从二项分布 ,且
,且 则
则 等于( )
等于( )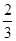

 .假设两人射击是否击中目标,相互之间没有影响; 每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少? (3)若甲连续射击5次,用ξ表示甲击中目标的次数,求ξ的数学期望Eξ.
.假设两人射击是否击中目标,相互之间没有影响; 每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少? (3)若甲连续射击5次,用ξ表示甲击中目标的次数,求ξ的数学期望Eξ. 上取一点P,使△PBC的面积大于
上取一点P,使△PBC的面积大于 的概率是____________
的概率是____________ ,则
,则 的值为( )
的值为( ) 


