题目内容
（本题满分14分）
已知箱中装有4个白球和5个黑球，且规定：取出一个白球的2分，取出一个黑球的1分．
现从该箱中任取 ( 无放回 ) 3个球，记随机变量X为取出3球所得分数之和．
(Ⅰ) 求X的分布列；
(Ⅱ) 求X的数学期望E(X)．
已知箱中装有4个白球和5个黑球，且规定：取出一个白球的2分，取出一个黑球的1分．
现从该箱中任取 ( 无放回 ) 3个球，记随机变量X为取出3球所得分数之和．
(Ⅰ) 求X的分布列；
(Ⅱ) 求X的数学期望E(X)．
(Ⅰ)所求X的分布列为
(Ⅱ) 所求X的数学期望E(X)为：
E(X)＝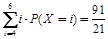
．
| X | 3 | 4 | 5 | 6 |
| P |  |  |  |  |
(Ⅱ) 所求X的数学期望E(X)为：
E(X)＝
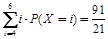．本题主要考查随机事件的概率和随机变量的分布列、数学期望等概念，同时考查抽象概括、运算能力，属于中档题．
（1）X的可能取值有：3，4，5，6，求出相应的概率可得所求X的分布列；
（2）利用X的数学期望公式，即可得到结论．
解：(Ⅰ) X的可能取值有：3，4，5，6．
； 
；
； 
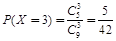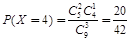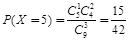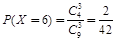． ………………8分
故所求X的分布列为
………………10分
(Ⅱ) 所求X的数学期望E(X)为：
E(X)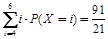＝． ………………14分
（1）X的可能取值有：3，4，5，6，求出相应的概率可得所求X的分布列；
（2）利用X的数学期望公式，即可得到结论．
解：(Ⅰ) X的可能取值有：3，4，5，6．
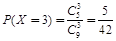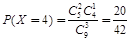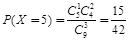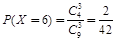； ； ； ． ………………8分故所求X的分布列为
| X | 3 | 4 | 5 | 6 |
| P | | | | |
(Ⅱ) 所求X的数学期望E(X)为：
E(X)＝
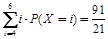． ………………14分
练习册系列答案
相关题目
个红球，
个白球（
，且
）；乙的箱子里面放有2个红球，1个白球，1个黄球．现在甲从自己的箱子里任取2个球，乙从自己的箱子里任取1个球．若取出的3个球颜色都不相同，则甲获胜．
的分布列．
上取一点P，使△PBC的面积大于
的概率是____________
，取到方片的概率是
与
，且乙投球2次均未命中的概率为
。
，求
的16名篮球运动员在某次训练比赛中的得分记录如下：
刚好是边长为
的等边三角形的三个顶点.
区域射击（不会打到
的概率为多少？（弹孔大小忽略不计）
内，调整一下后，又连打三枪，其成绩（环数）都在区间
内.现从这
次射击成绩中随机抽取两次射击的成绩（记为
和
）进行技术分析.求事件“
”的概率. 
，则
的值为（ ） 
