题目内容
16．若函数f（x）=$\frac{a-1{0}^{x}}{1+a•1{0}^{x}}$为奇函数，则实数a=1或-1．分析 函数f（x）=$\frac{a-1{0}^{x}}{1+a•1{0}^{x}}$为奇函数，可得f（-x）=-f（x），代入计算，可得a的值．
解答 解：∵函数f（x）=$\frac{a-1{0}^{x}}{1+a•1{0}^{x}}$为奇函数，
∴f（-x）=-f（x），
∴$\frac{a-1{0}^{-x}}{1+a•1{0}^{-x}}$=-$\frac{a-1{0}^{x}}{1+a•1{0}^{x}}$，
∴$\frac{a•1{0}^{x}-1}{1{0}^{x}+a}$=-$\frac{a-1{0}^{x}}{1+a•1{0}^{x}}$，
∴a=1或-1．
故答案为：1或-1．
点评 本题考查函数的奇偶性，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
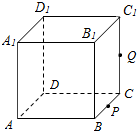如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则当CQ∈（0，$\frac{1}{2}$]∪{1}时，S为四边形；当CQ=$\frac{1}{2}$时S为等腰梯形；当CQ=1时，S的面积为$\frac{\sqrt{6}}{2}$．