题目内容
6．
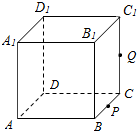如图，正方体ABCD-A1B1C1D1的棱长为1，P为BC的中点，Q为线段CC1上的动点，过点A，P，Q的平面截该正方体所得的截面记为S．则当CQ∈（0，$\frac{1}{2}$]∪{1}时，S为四边形；当CQ=$\frac{1}{2}$时S为等腰梯形；当CQ=1时，S的面积为$\frac{\sqrt{6}}{2}$．
分析 当CQ=1时，截面四边形是边长为$\frac{\sqrt{5}}{2}$的菱形，由此可求其面积．
解答 解：当CQ=1时，截面四边形是边长为$\frac{\sqrt{5}}{2}$的菱形，其对角线长为正方体的对角线长$\sqrt{3}$，另一条对角线长为面对角线长为$\sqrt{2}$，所以S=$\frac{1}{2}×\sqrt{2}×\sqrt{3}$=$\frac{\sqrt{6}}{2}$，
故答案为：$\frac{\sqrt{6}}{2}$．
点评 此题考查了截面的性质，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A，B的任意一点．
1．将函数y=sin（2x-θ）的图象F向右平移$\frac{π}{3}$个单位长度得到图象F′，若F′的一条对称轴是直线x=$\frac{π}{4}$，则θ的一个可能取值是（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{2}$ |
在三棱柱ABC-A1B1C1中，△ABC是边长为2正三角形，D、E分别是线段BB1、AC1的中点，DE⊥AC1．
如图所示的程序框图，运行相应的程序，若输入x的值为-4，则输出y的值为2．
15．已知一个正四面体纸盒的棱长为$2\sqrt{6}$，若在该正四面体纸盒内放一个正方体，使正方体可以在纸盒内任意转动，则正方体棱长的最大值为（ ）
| A． | 1 | B． | $\frac{{2\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |