题目内容
3.已知函数f(x)=lnx-a(1-1x1x) (a∈R).(1)求f(x)的单调区间;
(2)若f(x)的最小值为0,求a;
(3)在(2)的条件下,设数列{an}满足a1=1,an+1=f(an)-lnan+2,记[x]表示不大于x的最大整数,(如[3.1]=3),求Sn=[a1]+[a2]+…+[an].
分析 (1)利用导数,对a讨论,当a≤0时,当a>0时,即可求得f(x)的单调区间;
(2)(i)利用(Ⅰ)的结论即可求得a的值;
(3)利用归纳推理,猜想当n≥3,n∈N时,1<an<2,利用数学归纳法证明,即可得出结论.
解答 解:(1)由已知得f(x)定义域为(0,+∞) …(1分)
∵f?(x)=1x−ax2=x−ax1x−ax2=x−ax
当a≤0时,f?(x)>0∴f(x)的增区间是(0,+∞),无减区间.
当a>0时,x∈(0,a)时,f?(x)<0
x∈(a,+∞)时,f?(x)>0
∴f(x)的单调增区间为(a,+∞),单调减区间为(0,a) …(4分)
(2)由(1)知当a≤0时,f(x)无最小值
当a>0时,f(x)min=f(a)=lna-a+1=0∴a=1 …(6分)
(3)∵a=1∴f(x)=lnx+1x1x-1∴an+1=f(an)-lnan+2=1an1an+1 …(7分)
∵a1=1∴a2=2 a3=3232 a4=5353
下面证明当n≥3时,an∈(1,2)
1°当n=3时,a3=1212∴a3∈(1,2)
2°设an∈(1,2)∴1212<1an1an<1∴an+1∈(1,2)
综合1°,2°可知当n≥3时,an∈(1,2)…(10分)
∴[a1]=1[a2]=2[a3]=[a4]=…=[an]=1∴Sn={1;;;n=1n+1;;;n≥2..…(12分)
点评 本题主要考查函数的导数、导数的应用等基础知识,考查推理论证能力、运算求解能力、创新意识等,考查函数与方程思想、化归与转化思想、分类与整合思想、有限与无限思想等,属难题.

练习册系列答案
相关题目
14.已知函数y=log12(x2-ax+a)在(√2,+∞)上是减函数,则a的取值范围是( )
| A. | [2√2,4) | B. | [2√2,√2+2] | C. | (-∞,2√2] | D. | [2√2,+∞) |
8.定义在R上的偶函数f(x)满足f(x+2)-f(x)=0,且在[-1,0]上单调递增,设a=f(log32),b=f(-13log32),c=f(1912),则a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
12.已知函数f(x)=2ax3-3x2+1,若 f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( )
| A. | (1,+∞) | B. | (0,1) | C. | (-1,0) | D. | (-∞,-1) |
 如图,在△ABC中,AC=12,∠ABC=2∠C.
如图,在△ABC中,AC=12,∠ABC=2∠C.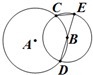 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.