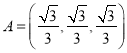题目内容
【题目】关于函数
，下列判断正确的是（ ）
A. 
有最大值和最小值
B. 的图象的对称中心为
（
）
C. 在
上存在单调递减区间
D. 的图象可由
的图象向左平移
个单位而得
【答案】B
【解析】分析：利用三角函数公式化简函数表达式，结合函数的图象与性质即可判断.
详解：函数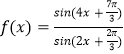
=
=
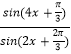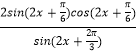
=2sin（2x+
）且sin（2x+
）≠0，
对于A：f（x）=2sin（2x+）存在最大值和不存在最小值．A不对；
对于B：令2x+=kπ，可得x=
，
∴f（x）的图象的对称中心为
（k∈Z），B对．
对于C：令
2x+
，可得
，
∴f（x）在
上不存在单调递减区间．
对于D：y=2sin2x的图象向左平移
个单位，可得2sin2（x
）=2sin（2x+），
但sin（2x+）≠0，
故选：B．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”，彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查，得到如下数据：
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
合计 | 15 | 12 | 13 | 7 | 8 | 45 |
（1）把每周使用移动支付6次及6次以上的用户称为“移动支付达人”，按分层抽样的方法，在我市所有“移动支付达人”中，随机抽取6名用户
求抽取的6名用户中，男女用户各多少人；
② 从这6名用户中抽取2人，求既有男“移动支付达人”又有女“移动支付达人”的概率.
（2）把每周使用移动支付超过3次的用户称为“移动支付活跃用户”，填写下表，问能否在犯错误概率不超过0.01的前提下，认为“移动支付活跃用户”与性别有关？
P(χ2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | .635 |
非移动支付活跃用户 | 移动支付活跃用户 | 合计 | |
男 | |||
女 | |||
合计 |
