题目内容
4.函数y=ln(x2)+x3的图象大致是( )| A. | 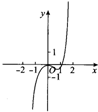 | B. | 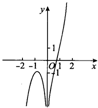 | C. | 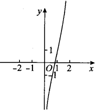 | D. | 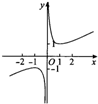 |
分析 根据函数的奇偶性即可排除D,根据函数的定义域即可排除A,C,根导数和函数的单调性的关系即可判断B正确.
解答 解:函数y=ln(x2)+x3为非奇非偶函数,故排除D,
函数的定义域为(-∞,0)∪(0,+∞),故排除A,C,
∵y′=$\frac{2}{x}$+x2=$\frac{3{x}^{3}+2}{x}$,
令y′=0,解得x=-$\sqrt{\frac{2}{3}}$>-1,
当y′>0时,即x<-$\sqrt{\frac{2}{3}}$或x>0时,函数单调递增,
当y′<0时,即-$\sqrt{\frac{2}{3}}$<x<0时,函数单调递减,
故选:B.
点评 本题考查了函数图象的识别,排除法时常用的方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.若曲线f(x)=$\frac{1}{3}$ax3+$\frac{1}{2}$bx2+cx+d(a,b,c>0)上不存在斜率为0的切线,则$\frac{f′(1)}{b}$-1的取值范围是( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
16.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F(c,0)关于直线y=$\frac{b}{c}$x的对称点Q在椭圆上,则椭圆的离心率是( )
| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}-1}{2}$ | D. | $\frac{3}{5}$ |
13.设i为虚数单位,复数$\frac{1+i}{2+bi}$为纯虚数,则实数b等于( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |