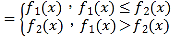Question

【题目】回答下列两个问题, 并给出例子或证明.

(1)对任意正整数, 在平面上是否都存在个不在同一条直线上的点, 使得任意两点间的距离都为正整数?

(2)在平面上是否存在两两不同的无限点列组成的点集, 使得内所有点不在同一条直线上, 且内任意两点间的距离为正整数?

Answer 1

【答案】（1）存在.（2）不存在

【解析】

（1）存在.

对于任意的（），取互不相同的个质数.

令，

显然，.

令，

于是，.

在轴上取点，在轴上取点，

易知，这个点，不在同一条直线上，且

为整数.

故为整数.

（2）不存在.

若不然, 假设存在不共线的无限点列组成的点集,且内任意两点间的距离都为正整数.取不共线的三点∈, 注意到,到之间的整数值.

而一到之间的整数值总共只有有限个,

由双曲线定义可知, 内除去三点的其余无限多个点必在以点A 和点B 为两个焦点的有限条互不相交的双曲线上, 称它们为AB 族双曲线.

同理, 内除去三点的其余无限多个点必在以点B 和点C 为两个焦点的有限条互不相交的双曲线上, 称它们为BC族双曲线.

由于三点不共线, 故两族双曲线的交点显然只有有限个.

然而,内除去三点的其余无限多个点中的每个点既在AB 族双曲线上,

又在BC 族双曲线上,从而, 必在两族双曲线的交点上.而两族双曲线的交点个数有限, 矛盾.