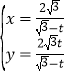题目内容
【题目】一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,若两只蚂蚁均从点A(1,0)同时逆时针匀速爬动,若红蚂蚁每秒爬过α角,黑蚂蚁每秒爬过β角(其中0°<α<β<180°),如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求α,β的值.
【答案】α=(![]() )°,β=(
)°,β=(![]() )°.
)°.
【解析】
试题确定α=![]() 180°,β=
180°,β=![]() 180°,m,n∈Z,利用2α,2β均为钝角,即可得到结论.
180°,m,n∈Z,利用2α,2β均为钝角,即可得到结论.
解:根据题意可知:14α,14β均为360°的整数倍,故可设14α=m360°,m∈Z,14β=n360°,n∈Z,从而可知α=![]() 180°,β=
180°,β=![]() 180°,m,n∈Z.
180°,m,n∈Z.
又由两只蚂蚁在第2秒时均位于第二象限,则2α,2β在第二象限.
又0°<α<β<180°,从而可得0°<2α<2β<360°,
因此2α,2β均为钝角,即90°<2α<2β<180°.
于是45°<α<90°,45°<β<90°.
∴45°<![]() 180°<90°,45°<
180°<90°,45°<![]() 180°<90°,
180°<90°,
即![]() <m<
<m<![]() ,
,![]() <n<
<n<![]() .
.
又∵α<β,∴m<n,从而可得m=2,n=3.
即α=(![]() )°,β=(
)°,β=(![]() )°.
)°.

练习册系列答案
相关题目