题目内容
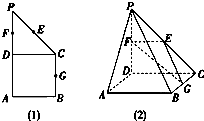
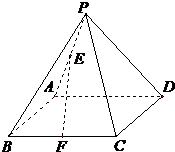
如图,在四面体ABCD中,平面EFGH分别平行于棱CD、AB,E、F、G、H分别在BD、BC、AC、AD上,且CD=a,AB=b,CD⊥AB.
(1)求证:四边形EFGH是矩形.
(2)设
=λ(0<λ<1),问λ为何值时,四边形EFGH的面积最大?
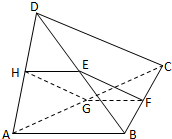
(1)求证:四边形EFGH是矩形.
(2)设
| DE |
| DB |

(1)证明:∵CD∥面EFGH,CD?平面BCD,
而平面EFGH∩平面BCD=EF.∴CD∥EF同理HG∥CD.∴EF∥HG
同理HE∥GF.∴四边形EFGH为平行四边形…(3分)
由CD∥EF,HE∥AB∴∠HEF(或其补角)为CD和AB所成的角,
又∵CD⊥AB.∴HE⊥EF.∴四边形EFGH为矩形.…..(6分)
(2)由(1)可知在△ABD中EH∥AB,∴
=
=λ,所以EH=λb,
在△BCD中EF∥CD,∴
=
=1-λ,所以EF=a(1-λ) …(8分)
又EFGH是矩形,故四边形EFGH的面积S=a(1-λ)•λb≤ab(
)2=
ab,当且仅当λ=1-λ,
即λ=
时等号成立,即E为BD的中点时,矩形EFGH的面积最大为
ab….(12分)
而平面EFGH∩平面BCD=EF.∴CD∥EF同理HG∥CD.∴EF∥HG
同理HE∥GF.∴四边形EFGH为平行四边形…(3分)
由CD∥EF,HE∥AB∴∠HEF(或其补角)为CD和AB所成的角,
又∵CD⊥AB.∴HE⊥EF.∴四边形EFGH为矩形.…..(6分)
(2)由(1)可知在△ABD中EH∥AB,∴
| DE |
| DB |
| EH |
| AB |
在△BCD中EF∥CD,∴
| BE |
| BD |
| EF |
| CD |
又EFGH是矩形,故四边形EFGH的面积S=a(1-λ)•λb≤ab(
| λ+1-λ |
| 2 |
| 1 |
| 4 |
即λ=
| 1 |
| 2 |
| 1 |
| 4 |

练习册系列答案
相关题目