题目内容
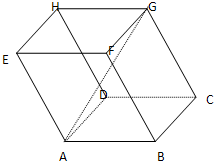
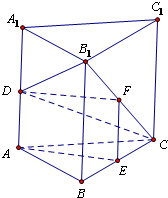
已知正三棱柱ABC-A1B1C1中，E是BC的中点，D是AA1上的一个动点，且
=m，若AE∥平面DB1C，则m的值等于______．
| AD |
| DA1 |
取B1C的中点E，连接EF、DF
∵△BB1C中，EF是中位线，∴EF∥B1B，
∵AD∥B1B，∴EF∥AD，可得EF、AD确定一个平面，设此平面为α
∵AE∥平面DB1C，AE?平面α，且平面DB1C∩α=DF
∴AE∥DF，结合EF∥AD得四边形AEFD是平行四边形
因此AD=EF=
A1A，可得D为A1A的中点
∴
=m=1
故答案为：1
∵△BB1C中，EF是中位线，∴EF∥B1B，
∵AD∥B1B，∴EF∥AD，可得EF、AD确定一个平面，设此平面为α
∵AE∥平面DB1C，AE?平面α，且平面DB1C∩α=DF
∴AE∥DF，结合EF∥AD得四边形AEFD是平行四边形
因此AD=EF=
| 1 |
| 2 |
∴
| AD |
| DA1 |
故答案为：1
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
