题目内容
【题目】如图，某三棱锥的正视图、侧视图和俯视图分别是直角三角形、等腰三角形和等边三角形，若该三棱锥的顶点都在同一球面上，则该球的表面积为（ ） 
A.27π
B.48π
C.64π
D.81π
【答案】C
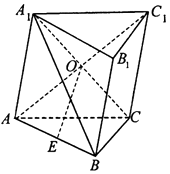
【解析】解：由三视图可知该几何体为三棱锥，棱锥的高VA=4，棱锥底面ABC是边长为6的等边三角形， 作出直观图如图所示：
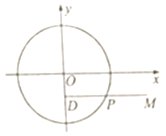
∵△ABC是边长为6的等边三角形，∴外接球的球心D在底面ABC的投影为△ABC的中心O，
过D作DE⊥VA于E，则E为VA的中点，
连结OA，DA，则DE=OA= 
=2 
，AE= 
VA=2，DA为外接球的半径r，
∴r= 
=4，
∴外接球的表面积S=4πr2=64π．
故选C．
【考点精析】掌握由三视图求面积、体积是解答本题的根本，需要知道求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积．
【题目】几个月前，成都街头开始兴起“mobike”、“ofo”等共享单车，这样的共享单车为很多市民解决了最后一公里的出行难题，然而，这种模式也遇到了一些让人尴尬的问题，比如乱停乱放，或将共享单车占为“私有”等． 为此，某机构就是否支持发展共享单车随机调查了50人，他们年龄的分布及支持发展共享单车的人数统计如表：
年龄 | [15，20） | [20，25） | [25，30） | [30，35） | [35，40） | [40，45） |
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展 | 4 | 5 | 12 | 9 | 7 | 3 |
（1）由以上统计数据填写下面的2×2列联表，并判断能否在犯错误的概率不超过0.1的前提下，认为年龄与是否支持发展共享单车有关系；
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
（2）若对年龄在[15，20）[20，25）的被调查人中随机选取两人进行调查，记选中的4人中支持发展共享单车的人数为X，求随机变量X的分布列及数学期望． 参考数据：
P（K2≥k） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式：K2= 
，其中n=a+b+c+d．
