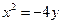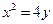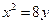题目内容
已知动圆P与定圆C:(x-2)2+y2=1相外切,又与定直线l:x=-1相切,那么动圆的圆心P的轨迹方程是( )
| A.y2=4x | B.y2=-4x | C.y2=8x | D.y2=-8x |
令P点坐标为(x,y),A(2,0),动圆得半径为r,
则根据两圆相外切及直线与圆相切得性质可得,PA=1+r,d=r,
P在直线的右侧,故P到定直线的距离是x+1,
所以PA-d=1,即
-(x+1)=1,
化简得:y2=8x.
故选C.
则根据两圆相外切及直线与圆相切得性质可得,PA=1+r,d=r,
P在直线的右侧,故P到定直线的距离是x+1,
所以PA-d=1,即
| (x-2)2+y2 |
化简得:y2=8x.
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
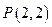 为
为 的中点,则抛物线C的方程为 .
的中点,则抛物线C的方程为 .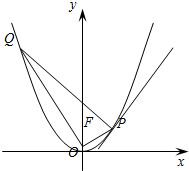
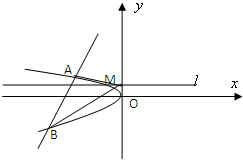
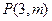 在以点
在以点 为焦点的抛物线
为焦点的抛物线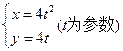 上,
上,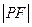 等于( )
等于( )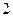
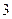
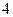
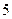
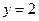 的抛物线的标准方程是( )
的抛物线的标准方程是( )