题目内容
4.设m∈R,函数f(x)=cosx(msinx-cosx)+cos2($\frac{π}{2}$-x),且f(-$\frac{π}{3}$)=f(0).(Ⅰ)求f(x)的单调递减区间;
(Ⅱ)设锐角△ABC的内角A、B、C所对的边分别为a、b、c,且$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}-{c}^{2}}$=$\frac{c}{2a-c}$,求f(A)的取值范围.
分析 (Ⅰ)现根据题意求得m,进而化简函数解析式,利用正弦函数的图象与性质确定单调减区间.
(Ⅱ)利用余弦定理和正弦定理对已知等式化简整理求得cosB,进而求得B,确定A的范围,则f(A)的取值范围可得.
解答 解:(I)f(x)=cosx(msinx-cosx)+cos2($\frac{π}{2}$-x)=$\frac{m}{2}$sin2x-cos2x,
由f(-$\frac{π}{3}$)=f(0)得:-$\frac{\sqrt{3}}{4}$m+$\frac{1}{2}$=-1,求得m=2$\sqrt{3}$,
∴f(x)=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$),
由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$得:kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$,k∈Z.
∴f(x)的单调递减区间为:[kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$],k∈Z.
(II)∵$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}-{c}^{2}}$=$\frac{c}{2a-c}$,由余弦定理得:$\frac{2accosB}{2abcosC}$=$\frac{c}{2a-c}$,
即整理得2acosB-ccosB=bcosC,由正弦定理得:
2sinAcosB-sinCcosB=sinBcosC,
2sinAcosB=sin(B+C)=sinA,cosB=$\frac{1}{2}$,
∴B=$\frac{π}{3}$.
∵△ABC锐角三角形,
∴$\frac{π}{6}$<A<$\frac{π}{2}$,$\frac{π}{6}$<2A-$\frac{π}{6}$<$\frac{5π}{6}$,
∴f(A)=2sin(2A-$\frac{π}{6}$)的取值范围为(1,2].
点评 本题主要考查了三角函数图象与性质,正弦定理和余弦定理的运用.考查了学生综合推理能力和一定的运算能力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | p∧q | B. | ¬p∧q | C. | ¬p∧¬q | D. | p∧¬q |
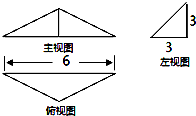
| A. | 6 | B. | 9 | C. | 12 | D. | 18 |
| M | 900 | 700 | 300 | 100 |
| y | 0.5 | 3.5 | 6.5 | 9.5 |
| M | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
(参考公式:$\hat y=\hat bx+\hat a$;其中$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{{x_i}^2}-n{{\overline x}^2}}}$,$\overline a=\overline y-\hat b\overline x$)
(2)小张开了一家洗车店,经统计,当M不高于200时,洗车店平均每天亏损约2000元;当M在200至400时,洗车店平均每天收入约4000元;当M大于400时,洗车店平均每天收入约7000元;根据表2估计小张的洗车店该月份平均每天的收入.
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4 |