题目内容
13.设函数f(x)=$\frac{{x}^{2}}{ax-2}$(a,b∈N*),且f(b)=b及f(-b)<-$\frac{1}{b}$成立,求f(x).分析 由已知中函数f(x)=$\frac{{x}^{2}}{ax-2}$(a,b∈N*),且f(b)=b,求出a,b的值,再由f(-b)<-$\frac{1}{b}$成立排除增根,可得答案.
解答 解:∵函数f(x)=$\frac{{x}^{2}}{ax-2}$(a,b∈N*),满足f(b)=b,
则$\frac{{b}^{2}}{ab-2}=b$,解得:b=0(舍去)或b=$\frac{2}{a-1}$,
则$\left\{\begin{array}{l}a=2\\ b=2\end{array}\right.$或$\left\{\begin{array}{l}a=3\\ b=1\end{array}\right.$,
又由f(-b)<-$\frac{1}{b}$成立,
∴$\frac{{b}^{2}}{-ab-2}<-\frac{1}{b}$,
经检验$\left\{\begin{array}{l}a=2\\ b=2\end{array}\right.$满足条件,但$\left\{\begin{array}{l}a=3\\ b=1\end{array}\right.$不满足条件,
故f(x)=$\frac{{x}^{2}}{2x-2}$
点评 本题考查的知识点是函数解析式的求法,函数的值,不等式的简单应用,是函数与不等式的简单综合考查,难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.数列$\frac{1}{1×4},\frac{1}{4×7},\frac{1}{7×10},…,\frac{1}{(3n-2)(3n+1)},…$的前10项和为( )
| A. | $\frac{27}{28}$ | B. | $\frac{9}{28}$ | C. | $\frac{30}{31}$ | D. | $\frac{10}{31}$ |
8.已知函数f(x)=mx2-mx+1,对一切实数x,f(x)>0恒成立,则m的范围为( )
| A. | [0,4] | B. | (0,4) | C. | (-∞,-4)∪(0,+∞) | D. | (-∞,-4)∪[0,+∞) |
5.若直线l沿x轴向左平移3各单位,再沿y轴向上平移1个单位后,回到原来的位置,则该直线l的斜率为( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
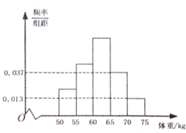 为了了解某校2015年高考准备报考“体育特长生”的学生体重情况,将所得数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前3个小组的频率之比为1:2:3,已知报考“体育特长生”的学生人数是48,则体重在[50,55)组的频数为( )
为了了解某校2015年高考准备报考“体育特长生”的学生体重情况,将所得数据整理后,画出了频率分布直方图,如图所示,已知图中从左到右的前3个小组的频率之比为1:2:3,已知报考“体育特长生”的学生人数是48,则体重在[50,55)组的频数为( )