题目内容
5.已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,记a=f(2-3),b=f(3m),c=f(log0.53),则( )| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
分析 由题意可得m=0,可得f(x)=2|x|-1在(0,+∞)单调递增,在(-∞,0)单调递减,比较三个变量的绝对值大小可得.
解答 解:∵定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数,
∴f(-1)=f(1),即2|-1-m|-1=2|1-m|-1,解得m=0,
∴f(x)=2|x|-1在(0,+∞)单调递增,在(-∞,0)单调递减,
∵2-3=$\frac{1}{8}$∈(0,1),3m=1,|log0.53|=log23>1,
∴f(2-3)<f(3m)<f(log0.53),即a<b<c
故选:A
点评 本题考查函数的单调性和奇偶性,属基础题.

练习册系列答案
相关题目
16.在△ABC中,$\overrightarrow{BA}$=(cos16°,sin16°),$\overrightarrow{BC}$=(2sin29°,2cos29°),则△ABC面积为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
13.已知集合A={x|x≤3,x∈R},B={x|x-1≥0,x∈N},则A∩B=( )
| A. | {0,1} | B. | {0,1,2} | C. | {2,3} | D. | {1,2,3} |
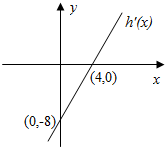 已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).
已知二次函数h(x)=ax2+bx+2,其导函数y=h′(x)的图象如图,f(x)=6lnx+h(x).