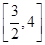题目内容
设函数 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 (
( ).
).
(1)求 的值;
的值;
(2)求 在
在 上的最大值;
上的最大值;
(3)当 时,
时, 对所有的
对所有的 及
及 恒成立,求实数的取值范围.
恒成立,求实数的取值范围.
 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 (
( ).
).(1)求
 的值;
的值;(2)求
 在
在 上的最大值;
上的最大值;(3)当
 时,
时, 对所有的
对所有的 及
及 恒成立,求实数的取值范围.
恒成立,求实数的取值范围.(1)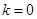 ;(2)
;(2)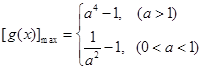 ;(3)
;(3)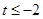 或
或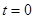 或
或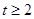 .
.
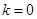 ;(2)
;(2)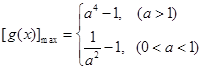 ;(3)
;(3)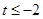 或
或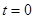 或
或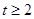 .
.试题分析:(1)根据
 为奇函数得到
为奇函数得到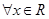 ,恒有
,恒有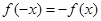 ,从而计算出
,从而计算出 的值;(2)根据指数函数的图像与性质对
的值;(2)根据指数函数的图像与性质对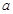 进行分类讨论确定函数
进行分类讨论确定函数 的单调性,从而由单调性求出
的单调性,从而由单调性求出 在
在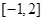 的最大值;(3)先根据(2)计算出
的最大值;(3)先根据(2)计算出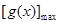 ,然后将不等式的恒成立问题转化成
,然后将不等式的恒成立问题转化成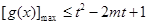 对
对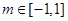 恒成立,接着构造关于
恒成立,接着构造关于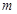 的函数
的函数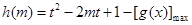 ,从而列出不等式组
,从而列出不等式组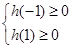 ,求解不等式即可得出
,求解不等式即可得出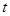 的取值范围.
的取值范围.试题解析:(1)由
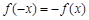 得
得 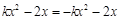 ,∴
,∴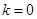 2分
2分(2)∵
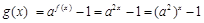 3分
3分①当
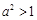 ,即
,即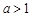 时,
时,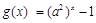 在
在 上为增函数
上为增函数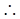
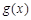 最大值为
最大值为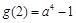 5分
5分②当
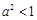 ,即
,即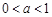 时,
时,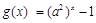 在
在 上为减函数
上为减函数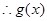 的最大值为
的最大值为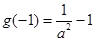 7分
7分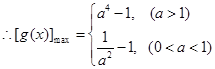 8分
8分(3)由(2)得
 在
在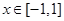 上的最大值为
上的最大值为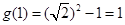
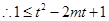 即
即 在
在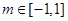 上恒成立 10分
上恒成立 10分令
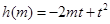
 即
即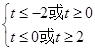
所以
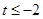 或
或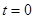 或
或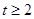 14分
14分
练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 ,求m和k的值.
,求m和k的值.
 恒成立,则实数x的值为 .
恒成立,则实数x的值为 .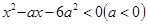 的解集为( )
的解集为( )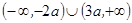
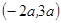
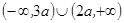
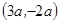
 ,例如:
,例如: ,
,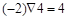 ,则函数
,则函数 的最大值为____________.
的最大值为____________.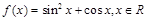 的最大值等于 .
的最大值等于 .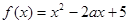 (
(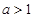 ),若
),若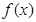 的定义域和值域均是
的定义域和值域均是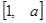 ,则实数
,则实数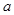 =
= 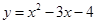 的定义域为
的定义域为 ,值域为
,值域为 ,则m的取值范围是( )
,则m的取值范围是( )