题目内容
如图,已知二次函数y=(x+m)2+k-m2的图象与x轴相交于两个不同的点A(x1,0)、B(x2,0),与y轴的交点为C.设△ABC的外接圆的圆心为点P.
(1)求⊙P与y轴的另一个交点D的坐标;
(2)如果AB恰好为⊙P的直径,且△ABC的面积等于 ,求m和k的值.
,求m和k的值.

(1)求⊙P与y轴的另一个交点D的坐标;
(2)如果AB恰好为⊙P的直径,且△ABC的面积等于
 ,求m和k的值.
,求m和k的值.
(1)(0,1) (2)k=-1,m=-2
解:(1)易求得点C的坐标为(0,k)
由题设可知x1,x2是方程(x+m)2+k-m2=0即x2+2mx+k=0的两根,
所以x1,2=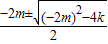 ,
,
所x1+x2=-2m,x1•x2=k(1分)
如图,∵⊙P与y轴的另一个交点为D,由于AB、CD是⊙P的两条相交弦,设它们的交点为点O,连接DB,
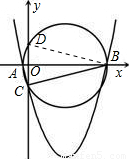
∴△AOC∽△DOB,则OD=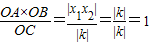 (2分)
(2分)
由题意知点C在y轴的负半轴上,从而点D在y轴的正半轴上,
所以点D的坐标为(0,1)(3分)
(2)∵AB⊥CD,AB又恰好为⊙P的直径,则C、D关于点O对称,
所以点C的坐标为(0,-1),
即k=-1(4分)
又AB=|x2-x1|=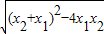 =
= ,
,
所以S△ABC= AB×OC=
AB×OC= ×2
×2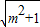 ×1=
×1= ,
,
解得m=±2.(正值舍去)
∴k=-1,m=-2.
由题设可知x1,x2是方程(x+m)2+k-m2=0即x2+2mx+k=0的两根,
所以x1,2=
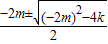 ,
,所x1+x2=-2m,x1•x2=k(1分)
如图,∵⊙P与y轴的另一个交点为D,由于AB、CD是⊙P的两条相交弦,设它们的交点为点O,连接DB,

∴△AOC∽△DOB,则OD=
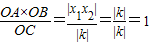 (2分)
(2分)由题意知点C在y轴的负半轴上,从而点D在y轴的正半轴上,
所以点D的坐标为(0,1)(3分)
(2)∵AB⊥CD,AB又恰好为⊙P的直径,则C、D关于点O对称,
所以点C的坐标为(0,-1),
即k=-1(4分)
又AB=|x2-x1|=
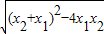 =
= ,
,所以S△ABC=
 AB×OC=
AB×OC= ×2
×2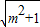 ×1=
×1= ,
,解得m=±2.(正值舍去)
∴k=-1,m=-2.

练习册系列答案
相关题目
 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 (
( ).
). 在
在 上的最大值;
上的最大值; 时,
时, 对所有的
对所有的 及
及 恒成立,求实数的取值范围.
恒成立,求实数的取值范围. 的顶点坐标为
的顶点坐标为 ,且
,且 的两个实根之差等于
的两个实根之差等于 ,
, __________.
__________.
 对任意的
对任意的 满足
满足 ,且当
,且当 时,
时, .若
.若 的取值范围是 .
的取值范围是 .