Question

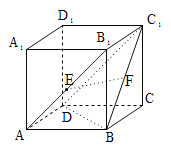
【题目】如图，PDCE为矩形，ABCD为梯形，平面PDCE⊥平面ABCD，∠BAD=∠ADC=90°，AB=AD=CD=1，PD=.

（1）若M为PA中点，求证:AC∥平面MDE；

（2）求直线PE与平面PBC所成角的正弦值.

（3）在PC上是否存在一点Q，使得平面QAD与平面PBC所成锐二面角的大小为.

Answer 1

【答案】（1）证明见解析（2）（3）存在

【解析】

（1）连结PC，交DE与N，可得N为PC中点，结合已知，可证MN∥AC，即可证明结论；

（2）建立空间直角坐标系，求出坐标，进而求出坐标及平面PBC法向量坐标，根据空间向量的线面角公式，即可求解；

（3）设，求出平面的法向量坐标，按照空间向量的面面角公式，求出，并判断是否满足条件.

（1）连结PC，交DE与N，连结MN，

∵△PAC中，M，N分别为两腰PA，PC的中点，

∴MN∥AC因为MN面MDE，又面MDE，

所以AC∥平面MDE

（2）∵∠ADC=90°，∴AD⊥DC，又AD平面ABCD，

平面PDCE∩平面ABCD，∴AD⊥平面PDCE，

又PD平面PDCE，∴AD⊥PD，以D为空间坐标系的原点，

分别以DA，DC，DP所在直线为x，y，z轴建立空间直角坐标系，

则，，

，设面PBC的法向量，应有即:

令，则，所以，

设PE与PBC所成角的大小为θ，∵，

∴，

直线PE与平面PBC所成角的正弦值.

（3）设则

，设平面QAD的法向量为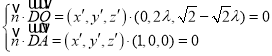，即:

则，令，则，所以

∵面PBC的法向量，

平面QAD与平面PBC所成锐二面角的大小为.∴，

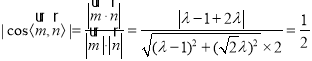整理得，解得或，

∴PC上存在点Q满足条件，Q与P重合，或.