题目内容
【题目】如图所示,在长方体ABCD﹣A1B1C1D1,若AB=BC,E,F分别是AB1,BC1的中点,则下列结论中不成立的是( )
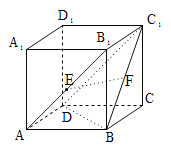
A.EF与BB1垂直B.EF⊥平面BDD1B1
C.EF与C1D所成的角为45°D.EF∥平面A1B1C1D1
【答案】C
【解析】
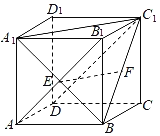
连A1B,则A1B交AB1于E,可证EF∥A1C1,再由长方体的垂直关系,可判断A正确;由已知可证A1C1⊥平面BDD1B1,可判断B为正确;EF∥A1C1,EF与C1D所成角就是∠A1C1D,∠A1C1D的大小不确定,判断C为错误; EF∥A1C1,可得D正确.
连A1B,则A1B交AB1于E,又F为BC1中点,
可得EF∥A1C1,由B1B⊥平面A1B1C1D1,
可得B1B⊥A1C1,可得B1B⊥EF,故A正确;
由EF∥A1C1,A1C1⊥平面BDD1B1,
可得EF⊥平面BDD1B1,故B正确;
EF与C1D所成角就是∠A1C1D,∵AA1 的长度不确定,
∴∠A1C1D的大小不确定,故C错误;
由E,F分别是AB1,BC1的中点,
得EF∥A1C1,可得EF∥平面A1B1C1D1,故D正确.
故选:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目