题目内容
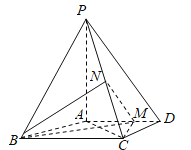
【题目】AB是圆O的直径,点C是圆O上异于AB的动点,过动点C的直线VC垂直于圆O所在平面,D,E分别是VA,VC的中点.
(1)判断直线DE与平面VBC的位置关系,并说明理由;
(2)当△VAB为边长为![]() 的正三角形时,求四面体V﹣DEB的体积.
的正三角形时,求四面体V﹣DEB的体积.
【答案】(1)![]() ⊥平面
⊥平面![]() ,理由见解析(2)
,理由见解析(2)![]()
![]()
【解析】
(1)由已知可得AC⊥BC,AC⊥VC,可证AC⊥平面VBC,D,E分别是VA,VC的中点,有DE∥AC,即可证明结论;
(2)由已知可证△VBC≌△VAC,得到BC=AC,进而求出BC,AC,VC值,利用等体积法有![]() ,即可求解.
,即可求解.
(1)DE⊥平面VBC,证明如下:
∵AB是圆O的直径,点C是圆O上异于AB的动点,
∴AC⊥BC,∵过动点C的直线VC垂直于圆O所在平面,
AC平面ABC,∴AC⊥VC,∵BC∩VC=C,
∴AC⊥平面VBC,∵D,E分别是VA,VC的中点,
∴DE∥AC,∴DE⊥平面VBC.
(2)∵△VAB为边长为![]() 的正三角形,
的正三角形,
AB是圆O的直径,点C是圆O上异于AB的动点,
过动点C的直线VC垂直于圆O所在平面,
D,E分别是VA,VC的中点,∴△VBC≌△VAC,∴BC=AC,∴BC2+AC2=AB2=8.∴AC=BC=2,![]()
D,E分别是VA,VC的中点,∴DE=![]() =1,
=1,
∴四面体V﹣DEB的体积为: ![]()
![]() =
=![]() .
.


练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目