题目内容
【题目】如图,圆
与长轴是短轴两倍的椭圆
:
相切于点
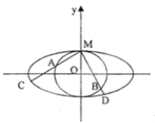
(1)求椭圆与圆的方程;
(2)过点
引两条互相垂直的两直线
与两曲线分别交于点
与点
(均不重合).若
为椭圆上任一点,记点到两直线的距离分别为
,求
的最大值,并求出此时的坐标.
【答案】（1）椭圆方程为
，圆的方程为
；（2）
的最大值为
，此时
.
【解析】
（1）根据
点坐标求得
，结合长轴是短轴两倍求得
，由此求得椭圆方程以及圆的方程.
（2）设出
点坐标，结合
以及矩形的几何性质求得的表达式，并由此求得的最大值，以及此时的坐标.
（1）由于
，所以
，由于椭圆长轴是短轴两倍，所以
，圆的半径为
，所以椭圆方程为，圆的方程为.
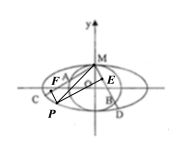
（2）设
，则
，
①，由于，设
如下图所示，所以四边形
是矩形，所以
，将①代入上式并化简得，
，因为
，所以当
时，取得最大值为，
，所以
，即.
练习册系列答案
相关题目
