题目内容
11.在极坐标系中,点(2,$\frac{π}{6}$)到直线$ρsin(θ-\frac{π}{6})=1$的距离是1.分析 把极坐标化为直角坐标,再利用点到直线的距离公式即可得出.
解答 解:点P(2,$\frac{π}{6}$)化为$x=2cos\frac{π}{6}$=$\sqrt{3}$,y=2$sin\frac{π}{6}$=1,∴P$(\sqrt{3},1)$.
直线$ρsin(θ-\frac{π}{6})=1$展开化为:$\frac{\sqrt{3}}{2}ρsinθ-\frac{1}{2}ρcosθ$=1,化为直角坐标方程为:$\sqrt{3}y-x-2=0$,即$x-\sqrt{3}y+2$=0.
∴点P到直线的距离d=$\frac{|\sqrt{3}-\sqrt{3}+2|}{\sqrt{{1}^{2}+(-\sqrt{3})^{2}}}$=1.
故答案为:1.
点评 本题考查了极坐标化为直角坐标的公式、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
3.已知$\overrightarrow{OA}$=$\overrightarrow{i}+3\overrightarrow{k}$,$\overrightarrow{OB}$=$\overrightarrow{j}+3\overrightarrow{k}$,则△OAB的面积为( )
| A. | $\frac{\sqrt{19}}{2}$ | B. | 2$\sqrt{19}$ | C. | $\sqrt{19}$ | D. | 8$\sqrt{19}$ |
1.某程序框图如图所示,该程序运行后输出的S的值是( )
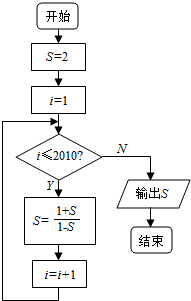

| A. | 2 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{2}$ |
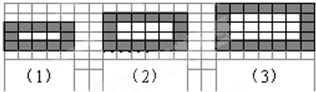 如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第1846个图案中需用黑色瓷砖7392块.
如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第1846个图案中需用黑色瓷砖7392块.