题目内容
设椭圆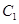 与抛物线
与抛物线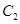 的焦点均在
的焦点均在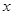 轴上,
轴上,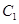 的中心及
的中心及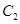 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
(Ⅰ)求曲线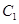 、
、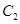 的标准方程;
的标准方程;
(Ⅱ)设直线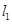 过抛物线
过抛物线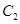 的焦点
的焦点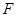 ,
,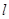 与椭圆交于不同的两点
与椭圆交于不同的两点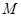 、
、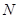 ,当
,当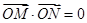 时,求直线
时,求直线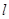 的方程.
的方程.
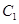 与抛物线
与抛物线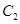 的焦点均在
的焦点均在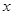 轴上,
轴上,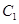 的中心及
的中心及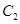 的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表:
的顶点均为原点,从每条曲线上各取两点,将其坐标记录于下表: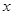 | 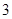 | 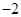 | 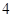 | 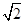 |
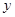 | 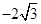 |  | 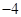 | 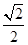 |
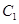 、
、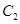 的标准方程;
的标准方程;(Ⅱ)设直线
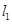 过抛物线
过抛物线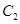 的焦点
的焦点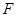 ,
,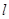 与椭圆交于不同的两点
与椭圆交于不同的两点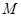 、
、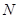 ,当
,当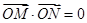 时,求直线
时,求直线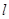 的方程.
的方程.(1)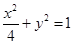 ,
,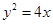
(2)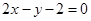 或
或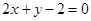
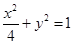 ,
,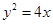
(2)
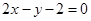 或
或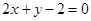
试题分析:解(1)由椭圆标准方程及抛物线标准方程可得出
点(-2,0)、(
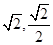 )是椭圆上两点
)是椭圆上两点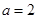

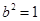
椭圆标准方程
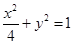
由点(3,
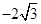 )、(4,-4)抛物线开口向右,其方程
)、(4,-4)抛物线开口向右,其方程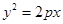
12=6P P=2
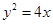 4分
4分(II)抛物焦点坐标F(1,0)
若直线
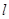 垂直于
垂直于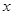 轴,方程
轴,方程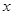 =1,由
=1,由 解故 M(1,
解故 M(1,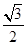 ),N(1,
),N(1,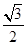 )
)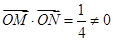 ∴
∴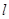 与
与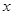 轴不垂直
轴不垂直设
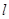 方程
方程 
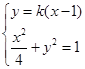 消去
消去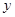 得:
得: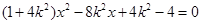
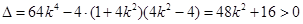
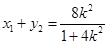
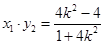
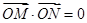
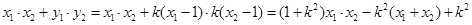
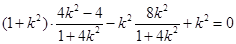
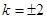
直线
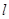 的方程
的方程 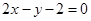 或
或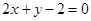 12分
12分点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
相关题目
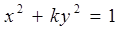 的离心率是2,则实数k的值是
的离心率是2,则实数k的值是 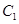 的焦点与椭圆
的焦点与椭圆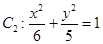 的右焦点重合,抛物线
的右焦点重合,抛物线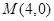 的直线
的直线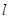 与抛物线
与抛物线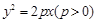 的焦点为
的焦点为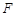 ,点
,点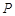 是抛物线上的一点,且其纵坐标为4,
是抛物线上的一点,且其纵坐标为4,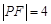 .
.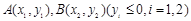 是抛物线上的两点,
是抛物线上的两点,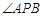 的角平分线与
的角平分线与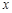 轴垂直,求直线AB的斜率;
轴垂直,求直线AB的斜率;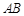 过点
过点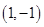 ,求弦
,求弦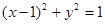 的切线(P点不在y轴上).
的切线(P点不在y轴上).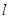 与(I)中的抛物线相交于M、N两点,问是否存在定点R,使
与(I)中的抛物线相交于M、N两点,问是否存在定点R,使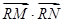 为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。
为常数?若存在,求出点R的坐标与常数;若不存在,请说明理由。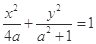 的离心率的最大值为( )
的离心率的最大值为( )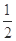
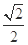

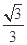
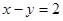 与抛物线
与抛物线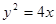 交于
交于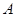 、
、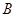 两点,则线段
两点,则线段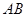 的中点坐标是 。
的中点坐标是 。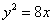 的焦点与双曲线
的焦点与双曲线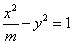 的右焦点重合,则双曲线的离心率为 .
的右焦点重合,则双曲线的离心率为 .