题目内容
【题目】某市将举办2020年新年大型花卉展览活动，举办方将建一块占地10000平方米的矩形展览场地ABCD，设计要求该场地的任何一边长度不得超过200米.场地中间设计三个矩形展览花圃①，②，③，其中花圃②与③是全等的矩形，每个花圃周围均是宽为5米的赏花路径.其中①号花圃的一边长度为25米.如图所示，设三个花圃占地总面积为S平方米，矩形展览场地的BC长为x米.
（1）试将S表示为x的函数，并写出定义域；
（2）问应该如何设计矩形场地的边长，使花圃占地总面积S取得最大值.
【答案】（1）
，
；（2）
，S取得最大值为7350.
【解析】
（1）花圃①的另一条边的长为
，花圃②与③一边的长为
，另一条边的长为
，求出3个矩形的面积后可得
关于
的函数解析式.
（2）利用基本不等式可求的最小值及何时取最小值.
（1）花圃①的另一条边的长为，
花圃②与③一边的长为，另一条边的长为，
所以
,
因为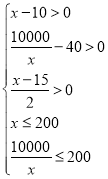
，故
，
故
，
.
（2）由基本不等式可得
，当且仅当时等号成立，
故当(米)时，
（
）.
答：当(米)时，（）.
阳光试卷单元测试卷系列答案
【题目】某市2011年至2017年新开楼盘的平均销售价格(单位：千元/平方米)的统计数据如下表：
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格 | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
（1）求
关于x的线性回归方程；
（2）利用（1）中的回归方程，分析2011年至2017年该市新开楼盘平均销售价格的变化情况，并预测该市2019年新开楼盘的平均销售价格。
附：参考公式： 
，
，其中
为样本平均值。
参考数据：
．
【题目】为了解某品种一批树苗生长情况，在该批树苗中随机抽取了容量为120的样本，测量树苗高度（单位：cm），经统计，其高度均在区间[19，31]内，将其按[19，21)，[21，23)，[23，25)，[25，27)，[27，29)，[29，31]分成6组，制成如图所示的频率分布直方图．其中高度为27 cm及以上的树苗为优质树苗．
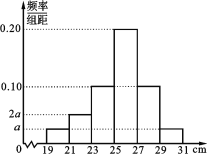
（1）求图中a的值；
（2）已知所抽取的这120棵树苗来自于A，B两个试验区，部分数据如下列联表：
A试验区 | B试验区 | 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整，并判断是否有99.9%的把握认为优质树苗与A，B两个试验区有关系，并说明理由；
（3）用样本估计总体，若从这批树苗中随机抽取4棵，其中优质树苗的棵数为X，求X的分布列和数学期望EX．
下面的临界值表仅供参考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：
，其中
．）
