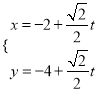题目内容
【题目】
在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系．已知点A的极坐标(
，
)，直线l的极坐标方程为ρcos(θ－)＝a，．
（1）若点A在直线l上，求直线l的直角坐标方程；
（2）圆C的参数方程为
(
为参数)，若直线
与圆C相交的弦长为，求
的值。
【答案】(1) 
(2) 
或
【解析】
试题（1）通过点A在直线l上，列出方程得到
，然后求解直线l的直角坐标方程（2）消去参数，求出
的普通方程，通过圆心到直线的距离半径半弦长的关系，即可求的值．
试题解析：（1）由点
在直线
上，可得=
所以直线
的方程可化为
从而直线的直角坐标方程为
.
（2）由已知得圆C的直角坐标方程为
所以圆C的圆心为（2，0），半径
，
而直线的直角坐标方程为
，若直线与圆C相交的弦长为
则圆心到直线的距离为
，所以
求得或
练习册系列答案
一本好题口算题卡系列答案
相关题目
