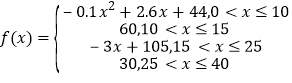题目内容
【题目】已知函数
.
（1）若对
，不等式
恒成立，求实数
的取值范围；
（2）记
，那么当
时，是否存在区间
使得函数在区间
上的值域恰好为
？若存在，请求出区间
；若不存在，请说明理由.
【答案】（Ⅰ）
；（Ⅱ）当
时，
，当
时，
，当
时，不存在区间.
【解析】
试题分析：（1）首先将问题转化为
对
恒成立，然后运用二次函数的图像与性质可得出满足题意实数
的条件，即可得出所求的答案；（2）首先将问题转化为
，然后由函数
在
上单调递增即可得出方程组，最后根据一元二次方程的根的情况判断其存在与不存在即可.
试题解析：(1) 
, 
，即对恒成立，则①
或②
，解得①
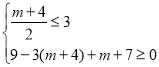或 ②
综合得m的取值范围为.
（注：亦可分离变量
对恒成立，）
（2）
，，,
，又
，∴
，∴在上单调递增，
，
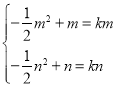，m,n是方程-
x2+(1-k)x=0的两根，x1=0,x2=2-2k
∴当时，，当时，，当时，不存在区间.
【题目】某公司计划在今年内同时出售变频空调机和智能洗衣机，由于这两种产品的市场需求量非常大，有多少就能销售多少，因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量，以使得总利润达到最大.已知对这两种产品有直接限制的因素是资金和劳动力，经调查，得到关于这两种产品的有关数据如下表：
资金 | 每台产品所需资金（百元） | 月资金供应量 （百元） | |
空调机 | 洗衣机 | ||
成本 | 30 | 20 | 300 |
劳动力（工资） | 5 | 10 | 110 |
每台产品利润 | 6 | 8 | |
试问：怎样确定两种货物的月供应量，才能使总利润最大？最大利润是多少?
【题目】（本小题满分14分）体育测试成绩分为四个等级：优、良、中、不及格．某班50名学生参加测试的结果如下：
等级 | 优 | 良 | 中 | 不及格 |
人数 | 5 | 19 | 23 | 3 |
（1）从该班任意抽取1名学生，求这名学生的测试成绩为“良”或“中”的概率；
（2）测试成绩为“优”的3名男生记为
，
，
，2名女生记为
，
．现从这5人中任选2人参加学校的某项体育比赛．
① 写出所有等可能的基本事件；
② 求参赛学生中恰有1名女生的概率．
