题目内容
6.已知f(x)=2ln(x+a)-x2-x在x=0处取得极值.(1)求实数a的值;
(2)证明:2ln($\frac{x}{2}+1$)-6≤(x+3)(x-2)
分析 (1)求出f(x)的导数,由题意可得,f′(0)=0,解方程可得a=2;
(2)由题意,证明2ln($\frac{x}{2}+1$)-6≤(x+3)(x-2)恒成立,可以构造函数g(x)=(x+3)(x-2)-2ln(1+$\frac{x}{2}$)+6,将证明不等式恒成立问题转化为函数g(x)≥0恒成立的问题,可利用导数求出函数的单调区间,确定出函数g(x)的最小值,若最小值大于等于0,则可得原不等式成立.
解答 (1)解:f(x)=2ln(x+a)-x2-x的导数为f′(x)=$\frac{2}{x+a}$-2x-1,
由于在x=0处取得极值,即有f′(0)=0,
即$\frac{2}{a}$-1=0,解得a=2;
(2)证明:由题意,设函数g(x)=(x+3)(x-2)-2ln(1+$\frac{x}{2}$)+6,
函数g(x)的定义域为(-2,+∞)
又g′(x)=2x+1-$\frac{2}{x+2}$=$\frac{2x(x+\frac{5}{2})}{x+2}$,
令g′(x)>0解得x>0,
令g′(x)<0解得-2<x<0.
又函数g(x)的定义域是(-2,+∞),
所以函数g(x)区间(-2,0)上是减函数,在(0,+∞)上是增函数
即有g(x)≥g(0)=0,
即有2ln($\frac{x}{2}+1$)-6≤(x+3)(x-2).
点评 本题考查导数的运用:求极值和单调区间,以及最值,主要考查函数的单调性的运用,注意构造函数运用最值证明不等式的方法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
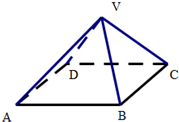 如图:正四棱锥V-ABCD中,高为2,底面ABCD是边长为4的正方形,则二面角V-AB-C的平面角为45°.
如图:正四棱锥V-ABCD中,高为2,底面ABCD是边长为4的正方形,则二面角V-AB-C的平面角为45°.