题目内容
1.已知函数f(x)=lnx-$\frac{a}{x}$(Ⅰ)当a=-1时,求f(x)的单调区间;
(Ⅱ)若f(x)在[1,e]上的最小值为$\frac{3}{2}$,求a的值;
(Ⅲ)若f(x)<x2在x∈(1,+∞)上恒成立,求a的取值范围.
分析 (Ⅰ)求出当a=-1时的f(x)解析式和导数,求得单调区间,注意函数的定义域;
(Ⅱ)求出导数,对a讨论,①若a≥-1,②若a≤-e,③若-e<a<-1,通过单调性求得最小值,解方程可得a的值;
(Ⅲ)运用参数分离,可得a>xlnx-x3,令g(x)=xlnx-x3,求得g(x)的值域,即可得到a的范围.
解答 解:(Ⅰ)当a=-1时,f(x)=lnx+$\frac{1}{x}$,
f(x)的定义域为(0,+∞),f′(x)=$\frac{x-1}{{x}^{2}}$,
则当x∈(0,1)时,f′(x)<0,x∈(1,+∞)时,f′(x)>0,
即有f(x)的增区间为(1,+∞),减区间为(0,1);
(Ⅱ)由题可知f′(x)=$\frac{x+a}{{x}^{2}}$,
①若a≥-1则x+a≥0,f(x)在[1,e]上为增函数,
[f(x)]min=f(1)=-a=$\frac{3}{2}$,即为a=-$\frac{3}{2}$(舍去);
②若a≤-e,则x+a≤0,f(x)在[1,e]上为减函数,
[f(x)]min=f(e)=1-$\frac{a}{e}$=$\frac{3}{2}$,a=-$\frac{e}{2}$(舍去);
③若-e<a<-1,令f′(x)=0,解得x=-a,
当1<x<-a时,f′(x)<0,f(x)在(1,-a)上为减函数;
当-a<x<e时,f′(x)>0,f(x)在(-a,e)上为增函数.
即有[f(x)]min=f(-a)=ln(-a)+1=$\frac{3}{2}$,解得a=-$\sqrt{e}$,
综上所述,a=-$\sqrt{e}$;
(Ⅲ)f(x)<x2,即lnx-$\frac{a}{x}$<x2,
又a>0,a>xlnx-x3,
令g(x)=xlnx-x3,h(x)=g′(x)=1+lnx-3x2,
h′(x)=$\frac{1}{x}$-6x=$\frac{1-6{x}^{2}}{x}$,
由x∈(1,+∞)时,h′(x)<0,h(x)在(1,+∞)上是减函数,
则h(x)<h(1)=-2<0,即g′(x)<0,
g(x)在(1,+∞)上递减,即有g(x)<g(1)=-1,
当a≥-1时,f(x)<x2在(1,+∞)上恒成立.
点评 本题考查导数的运用:求单调区间、极值和最值,主要考查不等式恒成立问题转化为求函数的最值问题,运用参数分离和函数的单调性是解题的关键.

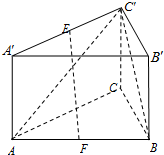 如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点.
如图,在三棱柱ABC-A′B′C′中,CC′⊥底面ABC,∠ACB=90°,AC=BC=CC′=a,E是A′C′的中点,F是AB的中点. 如图,在平面直角坐标系xOy中有一椭圆,椭圆方程为C:$\frac{{x}^{2}}{2}+{y}^{2}$=1.左右焦点分别F1(-1,0)和(1,0).设A,B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.求证:PF1+PF2是定值.
如图,在平面直角坐标系xOy中有一椭圆,椭圆方程为C:$\frac{{x}^{2}}{2}+{y}^{2}$=1.左右焦点分别F1(-1,0)和(1,0).设A,B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.求证:PF1+PF2是定值.